Not sure if this is user error: I am trying to evaluate the following integral:
var('t')
f = sqrt((e^(i * t) - 1) * (e^(-i*t) - 1))
show(f.integrate(t, 0, 2 * pi))
Sagemath returns 0, but WolframAlpha returns 8. Have I mis-specified the problem, or is this a bug?
A slight complement to Nasser's answer :
Contemplate :
sage: graphics_array(([f(t).demoivre(force=True).simplify_full().integrate(t, algorithm=u).plot((0,2*pi), title=u) for u in ("maxima", "giac", "fricas", "mathematica_free")]),ncols=2)
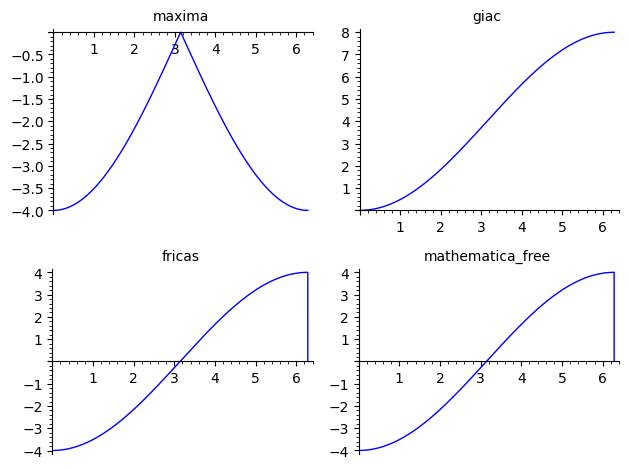
(sympy fails to integrate the expression).
maxima problems with various trig integrals have been documented for a long time... giac, fricas and mathematica give different expressions of similar functions (up to a constant), but proving the identities isn't trivlal (long algebrico/trigonometric massage ahead...).
But note :
sage: table([[u, f(t).demoivre(force=True).simplify_full().integrate(t, algorithm=u)] for u in ("maxima", "giac", "fricas", "mathematica_free")], header_row=["Algorithm", "Antiderivative"])
Algorithm Antiderivative
+------------------+---------------------------------------------------+
maxima -4/sqrt(sin(t)^2/(cos(t) + 1)^2 + 1)
giac -4*cos(1/2*t)*sgn(sin(1/2*t)) + 4*sgn(sin(1/2*t))
fricas -2*(cos(t) + 1)*sqrt(-2*cos(t) + 2)/sin(t)
mathematica_free -2*sqrt(-2*cos(t) + 2)*cot(1/2*t)
ALL those "CAS primitives" are periodic of period $2\pi$, whereas the function $\displaystyle\int_0^t f(t)\,dt$ is not ($f$ is positive except for a null-measure set ($t=2k\pi,\ k\in\mathbb{Z}$) where it is zero, therefore its integral is increasing). Computing the integral by taking limits of the primitive at bounds is wrong.
This happens to be plotted in the above figure for the fricas and mathematica cases. This (and the fact that it is not plotted for giac) is pure numerical happenstance...
Morality : never trust a CAS result without checking it...
HTH,
Mathematica is correct. You can see that easily by plotting the integrand from 0 to 2Pi. Clearly the area is not zero. It looks like about 8 is correct.
Here is a workaround in sagemath,
Write the integrand using trig function by converting it using Euler's formula. This will give sqrt(2-2*cos(t)) and now integrate this instead of the complex exponential. But make sure to use "fricas" as algorithm. The default algorithm and others give zero which is wrong.
var("t")
f = sqrt((e^(I * t) - 1) * (e^(-I*t) - 1))
g = expand(sageobj(f._maxima_().demoivre())).trig_simplify()
sqrt(-2*cos(t) + 2)
Now integrate the above, but use "fricas" to get correct answer
sage: integrate(g, t, 0, 2 * pi, algorithm="fricas")
8
Compare to
sage: integrate(g, t, 0, 2 * pi)
0
Asked: 2022-02-28 01:04:21 +0200
Seen: 571 times
Last updated: Feb 28 '22
Copyright Sage, 2010. Some rights reserved under creative commons license. Content on this site is licensed under a Creative Commons Attribution Share Alike 3.0 license.
See also https://trac.sagemath.org/ticket/17183.