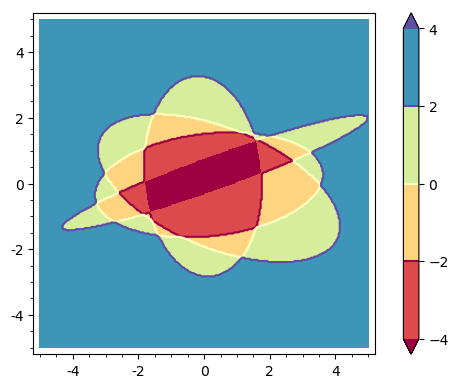
EDIT : The solution below is valid only for the special case presented here, not generally... I keep it here temporarily, but now think that there may not be a general solution.
Your question isn't as trivial as I thought initially. But your restriction:
without pre-calculating this area
points to a (semi-)trivial solution.
This restriction implies that you have at least a rough idea of the area where your intersectin might lie.
This rough idea might be obtained from a preliminary sketch. In your case:
sage: var("x,y")
(x, y)
sage: E1(x,y)=4.31814496201205*x^2 + 0.442360403122904*x*y + 0.0424448964961035*y
....: ^2 - 0.170411375833593*x - 0.0205526646997484*y - 2.4358560850288997
sage: E2(x,y)=7.81630506700337*x^2 - 47.0795923749769*x*y + 72.3295112191380*y^2
....: + 8.78879644990554*x - 27.0144183395227*y + 0.1289109700897777
sage: implicit_plot(E1,(-5,5),(-5,5))+implicit_plot(E2,(-5,5),(-5,5))

It can also be obtained analytically : the intersection of n ellipses is necessarily a subset of the intersection of the two first ellipses. The coordinates of the intersections can be obtained analytically:
sage: S=solve([E1(x,y),E2(x,y)],[x,y],solution_dict=True)
sage: S
[{x: 0.7393521295740851, y: 0.606115403583758},
{x: -0.7193521935219352, y: -0.2261153935996263},
{x: -0.7381518244093387, y: 0.1250916710319539},
{x: 0.7581518151815182, y: 0.254908323868246}]
sage: xmin=min([s.get(x) for s in S])
sage: xmax=max([s.get(x) for s in S])
sage: ymin=min([s.get(y) for s in S])
sage: ymax=max([s.get(y) for s in S])
Since all the coordinates are real, this intersection exists and isn't empty.region_plot can now be used to plot the intersectin of your ellipses (if it is not empty.
sage: region_plot(lambda x,y:E1(x,y)<0 and E2(x,y)<0, (xmin, xmax), (ymin, ymax),
....: plot_points=200)
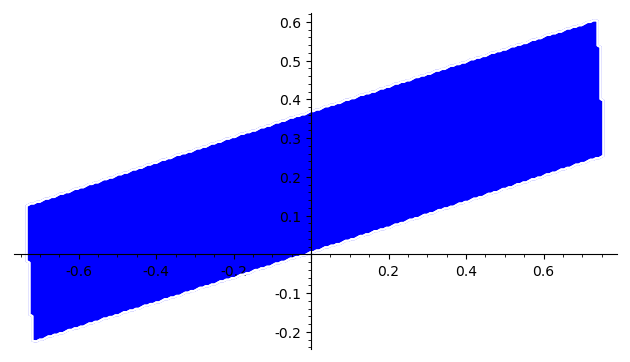
(One notes that, notwithstanding the plot_points=200 option, the sketch is relatively rough, and that its execution is slow. region_plot is a "brute-force" function...).
Of course, this solution is not really safisfactory: it will show you something ig the intersection of your n elipses is not empty, but this oinersection can be ridiculously small (i. e. invisible) if the intersection of your first two ellipses is small.
It is then probably better to compute the intersection of your ellipses before plotting it. This is not a trivial problem. ISTR that the geometry functions of Sgemath have a large section dedicated to polyhedra, a subject I know almost nothing about...
EDIT : vdelecroix comment is perfectly right : the proposed solution is but an approximation. And suffers counterexamples (think of an ellipse totally included in another : the edges have no intersection, and the intersection of the diks is the interior ellipse...).
HTH,