Revision history [back]
 | 1 | initial version |
Suppose that there are $k$ ellipses and let $R_i$ the bounded region limited by the $i$th-ellipse. Assume that $R_i$ is given by the relation $E_i(x,y)\leq0$. Consider the function $$S(x,y) = \sum_{i=1}^k \mathrm{sgn}(E_i(x,y)).$$ For $j=0,\ldots,k$, a point lying in the intersection of $j$ regions $R_i$ satisfies that $$S(x,y)=-j + (k-j)=k-2j.$$ So, one has to plot the contours of $S$ for the values $-k,-k+2,-k+4,\ldots,k$ to get the points lying in all regions $R_i$, in all but one regions, in all but two regions,..., in no region $R_i$, respectively. For example, consider the following code:
E1 = 3*x^2+5*x*y+8*y^2-2*x-30
E2 = x^2-5*x*y+7*y^2+x-3*y-2
E3 = 20*x^2+2*x*y+7*y^2+x-3*y-65
E4 = 6*x^2-5*x*y+28*y^2-2*x+3*y-70
fun = sum(sgn(EE) for EE in [E1,E2,E3,E4])
contour_plot(fun, (x,-5,5), (y,-5,5),contours=[-4,-2,0,2,4],
plot_points=300, fill=True, cmap="Spectral", colorbar=True)
It yields this image:
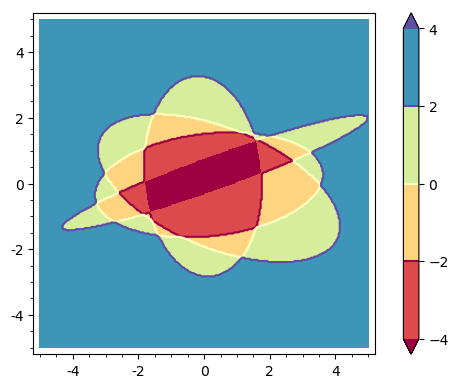
Blue points lie in no region bounded by an ellipse; green points lie in only one region; brown points lie in two regions; red points, in three regions; dark red points are the intersection of all regions $R_i$.
| | 2 | No.2 Revision |
Suppose that there are $k$ ellipses and let $R_i$ be the bounded region limited by the $i$th-ellipse. Assume that $R_i$ is given by the relation $E_i(x,y)\leq0$. Consider the function $$S(x,y) = \sum_{i=1}^k \mathrm{sgn}(E_i(x,y)).$$ For $j=0,\ldots,k$, a point lying in the intersection of $j$ regions $R_i$ satisfies that $$S(x,y)=-j + (k-j)=k-2j.$$ So, one has to plot the contours of $S$ for the values $-k,-k+2,-k+4,\ldots,k$ to get the points lying in all regions $R_i$, in all but one regions, in all but two regions,..., in no region $R_i$, respectively. For example, consider the following code:
E1 = 3*x^2+5*x*y+8*y^2-2*x-30
E2 = x^2-5*x*y+7*y^2+x-3*y-2
E3 = 20*x^2+2*x*y+7*y^2+x-3*y-65
E4 = 6*x^2-5*x*y+28*y^2-2*x+3*y-70
fun = sum(sgn(EE) for EE in [E1,E2,E3,E4])
contour_plot(fun, (x,-5,5), (y,-5,5),contours=[-4,-2,0,2,4],
plot_points=300, fill=True, cmap="Spectral", colorbar=True)
It yields this image:
Blue points lie in no region bounded by an ellipse; green points lie in only one region; brown points lie in two regions; red points, in three regions; dark red points are the intersection of all regions $R_i$. $R_i$.
| | 3 | No.3 Revision |
Suppose that there are $k$ ellipses and let $R_i$ be the bounded region limited by the $i$th-ellipse. Assume that $R_i$ is given by the relation $E_i(x,y)\leq0$. Consider the function $$S(x,y) = \sum_{i=1}^k \mathrm{sgn}(E_i(x,y)).$$ For $j=0,\ldots,k$, a point lying in the intersection of $j$ regions $R_i$ satisfies that $$S(x,y)=-j + (k-j)=k-2j.$$ So, one has to plot the contours of $S$ for the values $-k,-k+2,-k+4,\ldots,k$ to get the points lying in all regions $R_i$, in all but one regions, in all but two regions,..., in no region $R_i$, respectively. For example, consider the following code:
E1 = 3*x^2+5*x*y+8*y^2-2*x-30
E2 = x^2-5*x*y+7*y^2+x-3*y-2
E3 = 20*x^2+2*x*y+7*y^2+x-3*y-65
E4 = 6*x^2-5*x*y+28*y^2-2*x+3*y-70
fun = sum(sgn(EE) for EE in [E1,E2,E3,E4])
contour_plot(fun, (x,-5,5), (y,-5,5),contours=[-4,-2,0,2,4],
plot_points=300, fill=True, cmap="Spectral", colorbar=True)
It yields this image:
Blue points lie in no region bounded by an ellipse; green points lie in only one region; brown points lie in two regions; red points, in three regions; dark red points are the intersection of all regions $R_i$.
EDIT. In fact, a better and general approach is to plot the function $$S=\sum_{i=1}^k \mathbf{1}_{R_i},$$ where $\mathbf{1}_{R_i}$ stands for the characteristic function of $R_i$. The interesting contours are now $0,1,2,\ldots,k$.
For the above case, it is clear that $$\mathbf{1}_{R_i}(x,y)=\mathrm{unit\_step}(-E_i(x,y)).$$ Hence, with the same ellipses, the code
fun = sum(unit_step(-EE) for EE in [E1,E2,E3,E4])
contour_plot(fun, (x,-5,5), (y,-5,5), contours=[0..4],
plot_points=300, fill=True, cmap="Spectral_r", colorbar=True)
yields this figure:
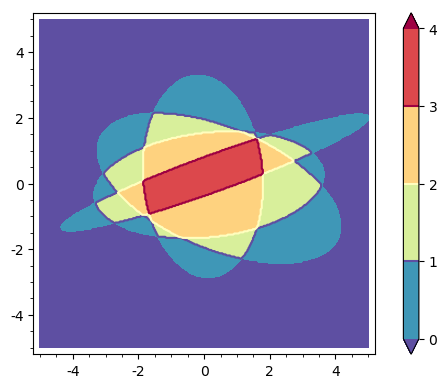
The color bar now directly says the number of regions to which a point belongs.
