Complement to Max's and Tolga's comments :
sage: var("t")
t
sage: with assuming(x>1): (e^(t^2)/sqrt(t)).integrate(t, 1, x^2)
-1/2*(-1)^(3/4)*gamma(1/4, -1) + 1/2*(-x^4)^(3/4)*gamma(1/4, -x^4)/x^3
$$ -\frac{1}{2} \, \left(-1\right)^{\frac{3}{4}} \Gamma\left(\frac{1}{4}, -1\right) + \frac{\left(-x^{4}\right)^{\frac{3}{4}} \Gamma\left(\frac{1}{4}, -x^{4}\right)}{2 \, x^{3}} $$
As you can see, this expression involves different inherently non-real complex factors (fractional powers of negative numbers, $\Gamma$ with negative arguments), whose sums happens to be real. The computation of the numerical value is inexact, so a small inexactitude is enough to result in a numerically non-zero imaginary part.
Showing that this imaginary part is zero seems out of reach of current CASses...
EDIT : To illistrate Max's comment about derivation :
sage: with assuming(x>1): foo=(e^(t^2)/sqrt(t)).integrate(t, 1, x^2) ; foo
-1/2*(-1)^(3/4)*gamma(1/4, -1) + 1/2*(-x^4)^(3/4)*gamma(1/4, -x^4)/x^3
sage: foo.diff(x)
-2*(-x^4)^(3/4)*D[1](gamma)(1/4, -x^4) - 3/2*gamma(1/4, -x^4)/(-x^4)^(1/4) - 3/2*(-x^4)^(3/4)*gamma(1/4, -x^4)/x^4
$$ -2 \, \left(-x^{4}\right)^{\frac{3}{4}} \mathrm{D}_{1}\left(\Gamma\right)\left(\frac{1}{4}, -x^{4}\right) - \frac{3 \, \Gamma\left(\frac{1}{4}, -x^{4}\right)}{2 \, \left(-x^{4}\right)^{\frac{1}{4}}} - \frac{3 \, \left(-x^{4}\right)^{\frac{3}{4}} \Gamma\left(\frac{1}{4}, -x^{4}\right)}{2 \, x^{4}} $$
One notes that Sage does not explicites a derivative of $\Gamma$ wrt one of its arguments...
Suspicious :
sage: giac.diff(*map(giac, (foo, x)))._sage_()
-3/2*gamma(1/4, -x^4)/(-x^4)^(1/4) - 3/2*(-x^4)^(3/4)*gamma(1/4, -x^4)/x^4 + 2*e^(x^4)
$$ -\frac{3 \, \Gamma\left(\frac{1}{4}, -x^{4}\right)}{2 \, \left(-x^{4}\right)^{\frac{1}{4}}} - \frac{3 \, \left(-x^{4}\right)^{\frac{3}{4}} \Gamma\left(\frac{1}{4}, -x^{4}\right)}{2 \, x^{4}} + 2 \, e^{\left(x^{4}\right)} $$
Highly suspicious :
sage: fricas.D(*map(fricas, (foo, x)))._sage_()
2*e^(x^4)
and, BTW :
sage: foo._sympy_().diff(x._sympy_())._sage_()
2*e^(x^4)
sage: foo._mathematica_().D(x).FullSimplify().sage()
2*e^(x^4)
But these expressions tun out to be equal :
sage: (fricas.D(*map(fricas, (foo, x)))._sage_()-giac.diff(*map(giac, (foo, x)))._sage_())
3/2*gamma(1/4, -x^4)/(-x^4)^(1/4) + 3/2*(-x^4)^(3/4)*gamma(1/4, -x^4)/x^4
sage: (fricas.D(*map(fricas, (foo, x)))._sage_()-giac.diff(*map(giac, (foo, x)))._sage_()).factor()
0
and comparing the Fricas result to a (rough) numerical estimate of the derivative of the function shows a very good agreement : their quotient is 1 up to $10^{-6}$ on the range (1, 4) :
sage: plot(lambda u:((Foo(u+1e-8)-Foo(u))/1e-8).real()/(2*e^(u^4))-1, (1, 4))
Launched png viewer for Graphics object consisting of 1 graphics primitive
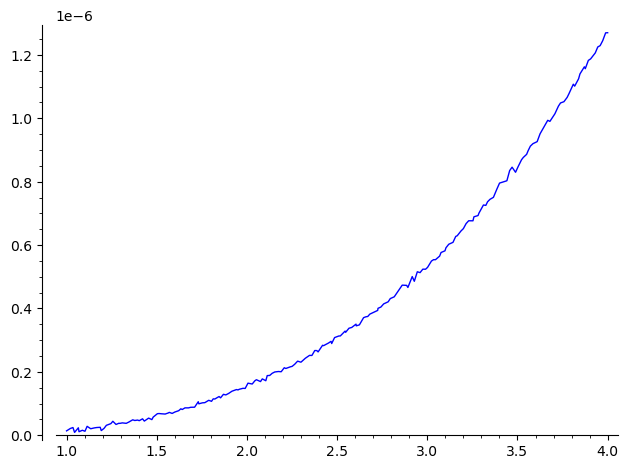
Mathematica's, Fricas' and Giac's derivations seem to be exact. The Sage's $\Gamma$ implementation may be perfected...
HTH,



This just means that approximation works in complex numbers here. Note that the imaginary part is negligible as compared to the real part, and so there is nothing wrong. Since you know that the result is real, you can use
f(4).numerical_approx().real()to get the appropriation in real numbers.This can be a workaround:
Also try this:
As you can see from the result (1.1842861526260861e+109, 4.7486208201754434e+95), the error bound is quite large. You can plot your integrand to see its behavior in the range of your interest.
[ Comment reposted as an answer... ]
Thank you. So nothing wrong with this function… But why I receive an error message if I try to differentiate it?!? I understand that this is not the original question though… :-)