Integral of a sum

edit

Using Maxima:

sage: maxima('assume(n>=0)')
sage: w = maxima('integrate(sum(t^(8*n),n,0,N),t,0,1)').sage()

sage: w
sum(1/(8*n + 1), n, 0, N)

sage: w.simplify_full()
-1/8*euler_gamma + 1/8*harmonic_number(N + 1/8) - 1/8*psi(1/8)

EDIT : @achrzesz 's solution is quite elegant and much better. As far as I understand, it relies on :

$$ \displaystyle{\int_{0}^{1} {\sum_{n=0}^{N} t^{8 \, n}}\,{d t} = {\sum_{n=0}^{N} \int_{0}^{1} t^{8 \, n}\,{d t}}} $$

Somehow, Maxima leverages this equality, wheareas Sage does not, while it recognises it :

sage: bool(integrate(sum(t^(8*n), n, 0, N, hold=True), t, 0, 1, hold=True)==sum(integrate(t^(8*n), t, 0, 1, hold=True), n, 0, N, hold=True))
True

I'm leaving my attempt to an answer here for the edification of future ask.sagemath.org (per-)users...

Well.. Sage (Giac in this case) may be wrong here.

Let's see what is this function :

sage: var("t, n, N")
(t, n, N)
sage: assume(N>0, t>0)
sage: g(t)=sum(t^(8*n), n, 0, N) ; g
t |--> (t^(8*N + 8) - 1)/(t^8 - 1)

One notes that : - g is undefined in 0, but continuous... - for positive t and positive integer N, g(t) is positive and increasing.

Let's get a "numerical feeling" :

sage: plot([g(t).subs(N=u).function(t) for u in (1..4)], (0, 11/10), legend_label=["N=%d"%u for u in (1..4)])

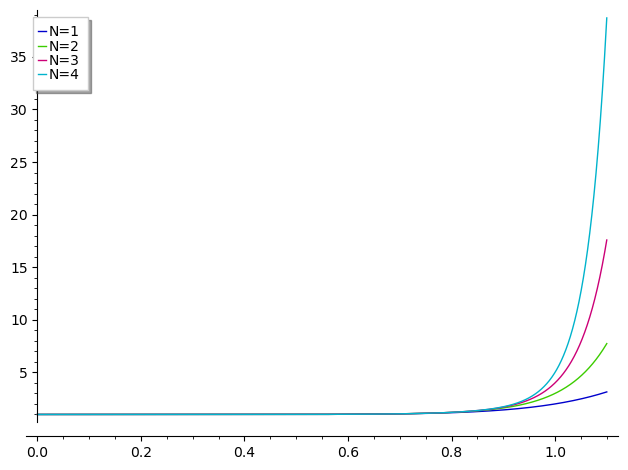
Ditto for the integral. Numerically :

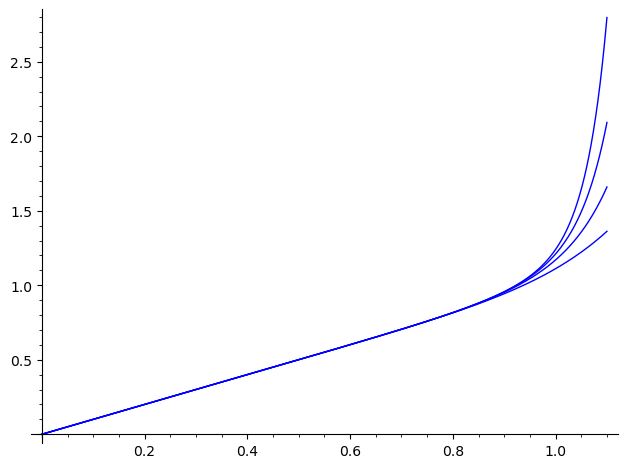
(for some reason, I have been unable to get the four functions on the same plot...).

These numerical explorations let us expect that the limit at t=1 is a function of N

Can we get an explicit expression of an antiderivative of g ? One can quickly check that neither Giac, Fricas nor Maxima have anithing useful to contribute :

sage: %time g(t).integrate(t, algorithm="giac")
CPU times: user 1.43 ms, sys: 151 µs, total: 1.58 ms
Wall time: 127 ms
integrate((t^(8*N + 8) - 1)/(t^8 - 1), t)
sage: %time g(t).integrate(t, algorithm="fricas")
CPU times: user 2.75 ms, sys: 0 ns, total: 2.75 ms
Wall time: 13.7 ms
integral((t^(8*N + 8) - 1)/(t^8 - 1), t)
sage: %time g(t).integrate(t, algorithm="maxima")
CPU times: user 79.1 ms, sys: 0 ns, total: 79.1 ms
Wall time: 58.5 ms
1/8*sqrt(2)*arctan(1/2*sqrt(2)*(2*t + sqrt(2))) + 1/8*sqrt(2)*arctan(1/2*sqrt(2)*(2*t - sqrt(2))) + 1/16*sqrt(2)*log(t^2 + sqrt(2)*t + 1) - 1/16*sqrt(2)*log(t^2 - sqrt(2)*t + 1) + 1/4*arctan(t) + integrate(t^8*t^(8*N)/(t^8 - 1), t) + 1/8*log(t + 1) - 1/8*log(t - 1)

[ Maxima's answer might be massaged to get a reccurence formula. I didn't pursue...].

Sympy has an answer ... untranslatable in Sage :

sage: %time sympy.integrate(*map(sympy.sympify, (g(t), t)))
CPU times: user 44.4 s, sys: 653 ms, total: 45.1 s
Wall time: 45.1 s
-N*t**9*t**(8*N)*lerchphi(t**8, 1, N + 9/8)*gamma(N + 9/8)/(8*gamma(N + 17/8)) - 9*t**9*t**(8*N)*lerchphi(t**8, 1, N + 9/8)*gamma(N + 9/8)/(64*gamma(N + 17/8)) - log(t - 1)/8 + log(t + 1)/8 - sqrt(2)*log(t**2 - sqrt(2)*t + 1)/16 + sqrt(2)*log(t**2 + sqrt(2)*t + 1)/16 + atan(t)/4 + sqrt(2)*atan(sqrt(2)*t - 1)/8 + sqrt(2)*atan(sqrt(2)*t + 1)/8

FWIW :

sage: sympy.lerchphi?
Init signature: sympy.lerchphi(*args)
Docstring:     
   Lerch transcendent (Lerch phi function).

   For \operatorname{Re}(a) > 0, |z| < 1 and s \in \mathbb{C}, the
   Lerch transcendent is defined as

      \Phi(z, s, a) = \sum_{n=0}^\infty \frac{z^n}{(n + a)^s},

   where the standard branch of the argument is used for n + a, and by
   analytic continuation for other values of the parameters.

[ and many more... ]

Does Sympy has anything to say about our limit ?

sage: sympy.limit(foo, t._sympy_(), 1)
oo

Hardly credible. Contradicts the numerical hint we've got...

Let's ask "the competition".

Asking Mathematica via Wlfram Alpha is somehow exploitable in Sage :

sage: G(t).limit(t=1)
limit(1/8*sqrt(2)*arctan(sqrt(2)*t + 1) + 1/8*sqrt(2)*arctan(sqrt(2)*t - 1) + 1/16*sqrt(2)*log(t^2 + sqrt(2)*t + 1) - 1/16*sqrt(2)*log(t^2 - sqrt(2)*t + 1) - 1/4*t^(8*N + 1)*hypergeometric((1, 4*N + 1/2), (4*N + 3/2,), -t^2)/(8*N + 1) - 1/2*t^(8*N + 1)*hypergeometric((1, 2*N + 1/4), (2*N + 5/4,), -t^4)/(8*N + 1) - 1/8*t^(8*N + 1)*hypergeometric((1, 8*N + 1), (8*N + 2,), -t)/(8*N + 1) - 1/8*t^(8*N + 1)*hypergeometric((1, 8*N + 1), (8*N + 2,), t)/(8*N + 1) + t^(8*N + 1)/(8*N + 1) + 1/4*arctan(t) + 1/8*log(t + 1) - 1/8*log(-t + 1), t, 1)

This is numerically more credible :

sage: sum(map(lambda u:plot(lambda v:G.subs(N=u)(t=v), (0, 11/10)), (1..4)))
Launched png viewer for Graphics object consisting of 20 graphics primitives

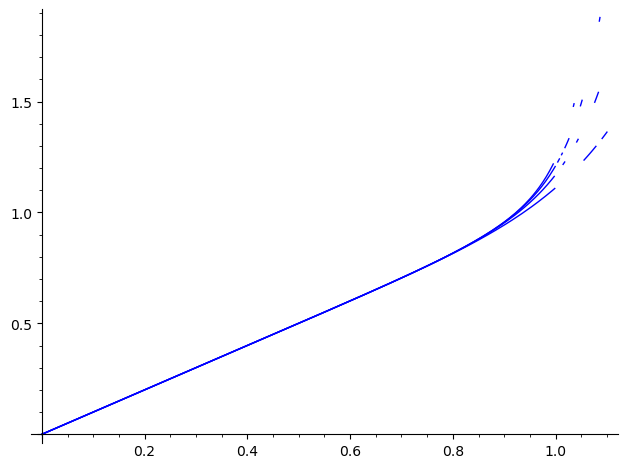
But the artefacts are a source of concern...

And Sage also gives this expression a hardly credible limit :

sage: G(t).limit(t=1)
limit(1/8*sqrt(2)*arctan(sqrt(2)*t + 1) + 1/8*sqrt(2)*arctan(sqrt(2)*t - 1) + 1/16*sqrt(2)*log(t^2 + sqrt(2)*t + 1) - 1/16*sqrt(2)*log(t^2 - sqrt(2)*t + 1) - 1/4*t^(8*N + 1)*hypergeometric((1, 4*N + 1/2), (4*N + 3/2,), -t^2)/(8*N + 1) - 1/2*t^(8*N + 1)*hypergeometric((1, 2*N + 1/4), (2*N + 5/4,), -t^4)/(8*N + 1) - 1/8*t^(8*N + 1)*hypergeometric((1, 8*N + 1), (8*N + 2,), -t)/(8*N + 1) - 1/8*t^(8*N + 1)*hypergeometric((1, 8*N + 1), (8*N + 2,), t)/(8*N + 1) + t^(8*N + 1)/(8*N + 1) + 1/4*arctan(t) + 1/8*log(t + 1) - 1/8*log(-t + 1), t, 1)
sage: G(t).limit(t=1).simplify()
Infinity

Last resort : Ask "the competition directly :

sage: %time LM=g(t)._mathematica_().Integrate(t).Limit(t._mathematica_().Rule(1)).FullSimplify().sage() ; LM
CPU times: user 5.1 ms, sys: 0 ns, total: 5.1 ms
Wall time: 565 ms
1/16*(pi*(8*N + 1)*(sqrt(2) + 1) + sqrt(2)*(8*N + 1)*log(2) + 16*sqrt(2)*N*log(1/2*sqrt(2) + 1) + 16*N*log(2) + 2*sqrt(2)*log(1/2*sqrt(2) + 1) + 2*log(2) + 16)/(8*N + 1) + 1/8*harmonic_number(8*N) - 1/16*harmonic_number(4*N) + 1/16*harmonic_number(4*N - 1/2) - 1/16*harmonic_number(2*N - 1/4) + 1/16*harmonic_number(2*N - 3/4) - 1/16*harmonic_number(N - 3/8) + 1/16*harmonic_number(N - 7/8)

This result seems to be concordant with the numerical feelings we've got :

sage: [LM.subs(N=u).n() for u in (1..4)] 
[1.11111111111111, 1.16993464052288, 1.20993464052288, 1.24023767082591]

Sorry for being unable to find an alternative...

HTH,