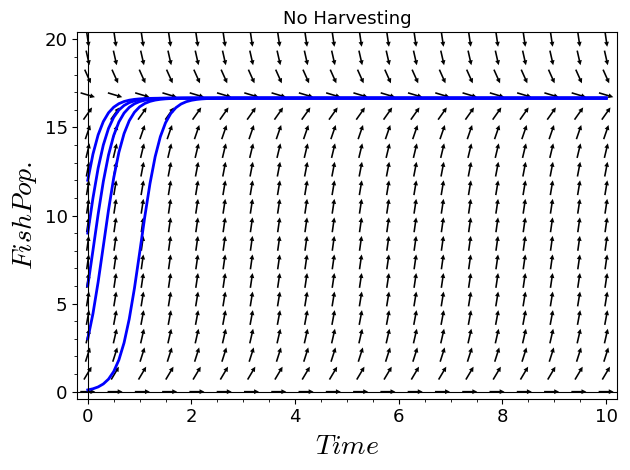
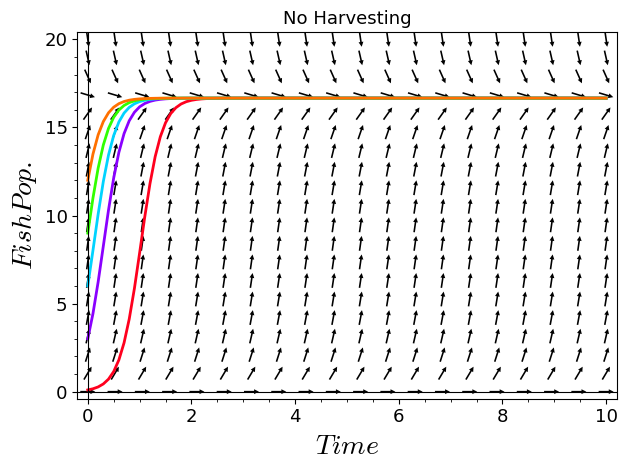
I'm having trouble plotting this population differential equation with five particular solutions all on the same graph. Please help.
Here is some code
x,t = var('x,t')
plot1 = plot_slope_field(5*x-.3*x^2-0*t,(t,0,10),(x,0,20),headaxislength=3,headlength=3,axes_labels=['$Time$','$Fish Pop.$'],title="No Harvesting",fontsize=13)
x = function('x')(t)
soln = lambda c:desolve_rk4(diff(x,t)==5*x-.3*x^2-0*t,x,ics=[0,c],end_points=[0,10],ivar=t,step=0.1)
plot2 = lambda c:list_plot(soln(c),plotjoined=True,axes_labels=['$Time$','$Fish Pop.$'],thickness=2)
show(plot1+plot2(12),ymin=0,ymax=20)
Referencing the last line of code, I wish to input .1, 3, 6, 9, and 12 all at the same time.