Here's elements of Symmetric group of 6th order: S3:
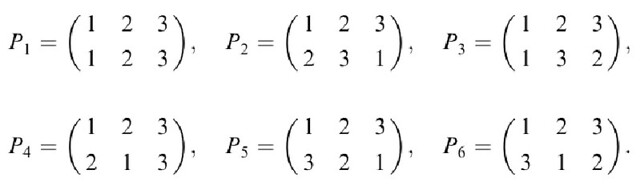
I want to check that P3*P6=P4.
G = SymmetricGroup(3)
BookNumbers = [1, 4, 2, 3, 6, 5]
P = [0]
for i in BookNumbers:
P.append(sorted(G.list())[i-1])
print (P[3] * P[6]).list(), P[4].list()
print (P[3] * P[6]) == P[4]
it gives:
[3, 2, 1] [2, 1, 3]
False
so they are the same actually. But how do I make sage say True?.
The problem is that you are comparing lists, not Sage objects. achrzesz gives an answer which compares two Sage group elements, so they are equal. The lists you give are simple Python ordered lists, and as ordered things, certainly aren't the same. Why didn't you just compare P[3]*P[6] and P[4]?
By the way, they're not the same. But that's a different issue. They're using the notation of the second row of your notation in your original question, not cycle notation.
sage: P[3] * P[6]
(1,3)
sage: P[4]
(1,2)
sage: G = SymmetricGroup(3)
sage: P3=G((3,2))
sage: P6=G((3,1,2))
sage: P4=G((2,1))
sage: P3*P6==P4
True
Asked: 2012-06-12 14:18:09 +0100
Seen: 345 times
Last updated: Jun 12 '12
Copyright Sage, 2010. Some rights reserved under creative commons license. Content on this site is licensed under a Creative Commons Attribution Share Alike 3.0 license.
