S3's elements
Here's elements of Symmetric group of 6th order: S3:
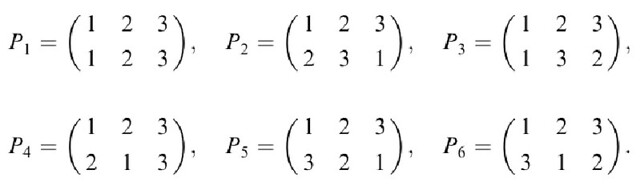
I want to get the same in Sage. So I do:
sage: G = SymmetricGroup(3)
sage: G.list()
[(), (2,3), (1,2), (1,2,3), (1,3,2), (1,3)]
Now I can't find (1,3,2) element in the book. As far as I understand:
P1 -> ()
P2 -> (1,2,3)
P3 -> (2,3)
P4 -> (1,2)
P5 -> (1,3)
P6 -> ??? also (1,2,3) ???
So my question is to set the correct map from sage to my book...

