Test if a graph has a claw-decomposition

graphtheory

licheng
311 ●6 ●25 ●43

Given two graphs $F$ and $G$ , an $F$ -decomposition of $G$ is a partition of the edges of $G$ into subgraphs isomorphic to $F$ .

First, I am very interested in the case where $F$ is a special subgraph, particularly when F is a claw (i.e. $K_{1,3}$ , that is, determining whether a graph has a claw-decomposition. If so, return true and provide a specific decomposition scheme.

For example, the first graph in the following figure has no decomposition (shown for example in M. Hasanvand The existence of planar 4-connected essentially 6-edge-connected graphs with no claw-decompositions. Graphs and Combinatorics, 2023, 39(1): 1. The second graph in the following figure has a claw-decomposition, shown by the four distinct colorings.

I am wondering whether it is possible to write a program to check if a graph has a claw-decomposition. A further question is whether there is a general method for arbitrary subgraphs.

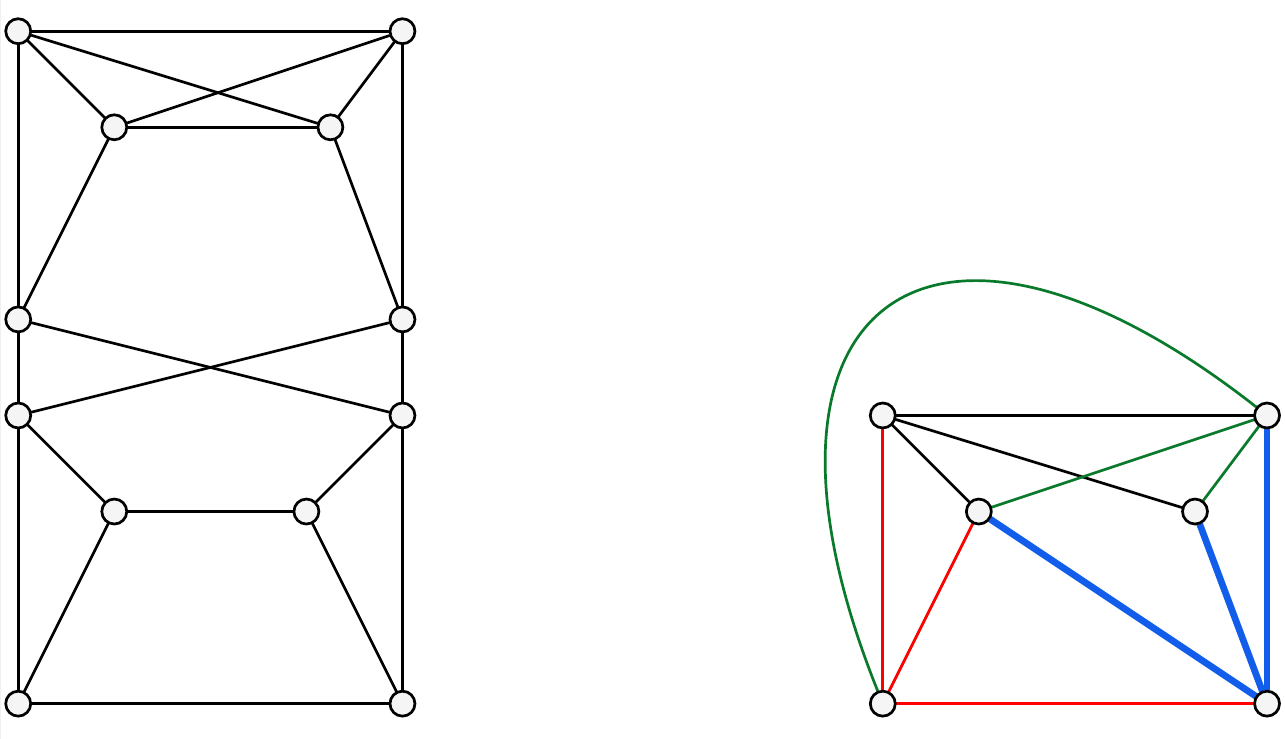
image description

The above two graphs in sage format:

Graph( [(0, 1), (0, 2), (0, 3), (0, 4), (1, 2), (1, 3), (1, 5), (2, 3), (2, 4), (3, 5), (4, 6), (4, 7), (5, 6), (5, 7), (6, 8), (6, 10), (7, 9), (7, 11), (8, 9), (8, 10), (9, 11), (10, 11)])


Graph([(0, 1), (0, 2), (0, 3), (0, 4), (1, 2), (1, 3), (1, 4), (1, 5), (2, 4), (2, 5), (3, 5), (4, 5)])

add a comment

2 Answers

Sort by » oldest newest most voted

answered 0 years ago

Max Alekseyev

6922 ●9 ●52 ●161

updated 0 years ago

This problem is best solved with integer programming. Here is my solution, which you can also run at Sagecell:

import itertools
from sage.numerical.mip import MIPSolverException

def find_claw_decomposition(G):

    # quick check
    if G.size()%3: 
        print('Size is not a multiple of 3')
        return None

    milp = MixedIntegerLinearProgram()

    # indicator variables: att[(edge,node)] = 1 iff edge is part of claw rooted at node
    att = milp.new_variable(binary=True)
    # rat[v] = number of claws rooted at v
    rat = milp.new_variable(integer=True)

    # each edge should be attached to one of its endpoints
    for e in G.edges(labels=False):
        milp.add_constraint( att[(e,e[0])] + att[(e,e[1])] == 1 )

    # each node should have a multiple of 3 attached edges
    for v in G.vertices():
        milp.add_constraint( sum( att[(e,v)] for e in G.edges_incident(v,labels=False) ) == 3 * rat[v] )

    try:
        milp.solve()
    except MIPSolverException:
        print('No decomposition exists.')
        return None

    claws = []
    A = milp.get_values(att,convert=bool,tolerance=1e-6)

    for v in G.vertices():
        it = filter(lambda e: A[(e,v)], G.edges_incident(v,labels=False))
        while ( claw := tuple(itertools.islice(it,3)) ):
            claws.append(claw)

    return claws

For example, running on your second graph:

G = Graph([(0, 1), (0, 2), (0, 3), (0, 4), (1, 2), (1, 3), (1, 4), (1, 5), (2, 4), (2, 5), (3, 5), (4, 5)])
find_claw_decomposition(G)

produces the following decomposition:

[((0, 1), (0, 2), (0, 3)),
 ((1, 2), (1, 3), (1, 5)),
 ((0, 4), (1, 4), (2, 4)),
 ((2, 5), (3, 5), (4, 5))]

link

add a comment

answered 0 years ago

Sébastien
3321 ●8 ●44 ●91 http://www.slabbe.org/

updated 0 years ago

This is a typical universal cover problem which can be solved using Knuth dancing links' algorithm:

def has_claw_decomposition(G, certificate=False):
    import itertools
    from sage.combinat.matrices.dancing_links import dlx_solver

    id_to_edge = [frozenset(edge) for edge in G.edges(labels=False)]
    edge_to_id = {edge:i for (i,edge) in enumerate(id_to_edge)}

    rows = []    
    for u in G:
        u_neighbors = G.neighbors(u)
        for three_neighbors in itertools.combinations(u_neighbors, 3):
            L = [edge_to_id[frozenset((u,v))] for v in three_neighbors]
            L.sort()
            rows.append(L)
    d = dlx_solver(rows)

    solution = d.one_solution()
    has_solution = not solution is None
    if not certificate:
        return has_solution
    else:
        if has_solution:
            solution_vertices = [[tuple(id_to_edge[id]) for id in rows[row_number]]
                                 for row_number in solution]
            return (has_solution, solution_vertices)
        else:
            return (has_solution, solution)

The first graph:

sage: from slabbe.graph import has_claw_decomposition
sage: G1 = Graph( [(0, 1), (0, 2), (0, 3), (0, 4), (1, 2), (1, 3),
....: (1, 5), (2, 3), (2, 4), (3, 5), (4, 6), (4, 7), (5, 6), (5, 7), (6, 8),
....: (6, 10), (7, 9), (7, 11), (8, 9), (8, 10), (9, 11), (10, 11)])
sage: has_claw_decomposition(G1)
False
sage: has_claw_decomposition(G1, certificate=True)
(False, None)

The second graph:

sage: G2 = Graph([(0, 1), (0, 2), (0, 3), (0, 4), (1, 2), (1, 3), (1, 4),
....:    (1, 5), (2, 4), (2, 5), (3, 5), (4, 5)])
sage: has_claw_decomposition(G2)
True
sage: has_claw_decomposition(G2, certificate=True)     # random
(True,
 [[(0, 1), (1, 2), (1, 5)],
  [(0, 3), (1, 3), (3, 5)],
  [(0, 2), (2, 4), (2, 5)],
  [(0, 4), (1, 4), (4, 5)]])

Actually, I wrote the code as a new function inside the graph module of my package. It could move up to sage if it is desirable, perhaps once it is generalized to any subgraph, for instance using the graph method subgraph_search_iterator().

Note that dancing links allows to enumerate/count all solutions. Also, there is a method to solve the dlx using sat solvers or milp solvers. See the documentation of dlx solver in sagemath here for more information.

link

Comments

See https://github.com/sagemath/sage/pull... for adding in SageMath the decomposition into any subgraphs.

Sébastien ( 0 years ago )

Note an overhead if a vertex degree $d$ is large - one would need to include $\binom{d}3$ potential claws into consideration. The ILP-based approach given in my answer is free from this issue since it cares only about the number of edges assigned to claws rooted at a vertex being a multiple of 3, but not about how exactly they are partitioned into claws.

Btw, another alternative to solving the exact cover problem is to use Cliquer interface on a graph where vertices are claws in the given graph and two claws are connected if they are edge-disjoint.

Max Alekseyev ( 0 years ago )

Interesting! Thanks for the remark!

Sébastien ( 0 years ago )

add a comment

Your Answer

Please start posting anonymously - your entry will be published after you log in or create a new account.

Add Answer

Test if a graph has a claw-decomposition

2 Answers

Comments

Your Answer

Question Tools

Stats

Related questions

Test if a graph has a claw-decomposition savecancel

2 Answers

Comments

Your Answer

Question Tools

Stats

Related questions

Test if a graph has a claw-decomposition