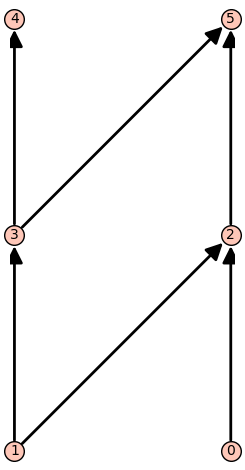
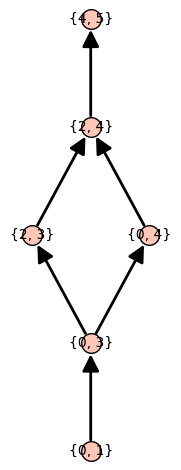
Lattice of maximum-length antichains in sage
The Dilworth lattice of a poset $P$ is the lattice of maximum length antichains in $P$, where two such antichains have $A \leq B$ if and only if every member of $A$ is less than or equal to some member of $B$.
Question: Is there an easy way to obtain the Dilworth lattice of a given poset using Sage?
Here my attempt:
P=posets.PentagonPoset()
A = P.antichains()
O=Poset((A,lambda v,w:v<=w))
I do not know how to define the right order on A in an easy way. It seems that <= is the wrong order, but even then it gives an error.