Not getting correct output while computing posets with some conditions.
I want to compute finite posets on 6 elements. Also, I want the following conditions on the posets: 2 covers 0, 4 covers 2, 3 covers 1, 5 covers 3. Also, 0, 1 are incomparable and 4, 5 are incomparable. For that I am giving the following commands:
A=[]
P = Posets(6)
for p in P:
if p.covers(0, 2) and p.covers(2, 4) and p.covers(1, 3) and p.covers(3, 5) and p.compare_elements(1, 0) is None and p.compare_elements(4, 5) is None:
A.append(p);
print(A)
The output I am getting is not correct. There is only one element in sage output but that is not true. Is there any issue with my code?
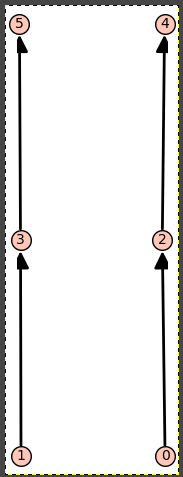

My impression is that the assumption on the element labels may be causing the unexpected result. That is,
Pis a list of non-isomorphic posets on 6 elements. So for each poset it contains only one possible labeling.Perhaps iterating over all possible element labelings for each poset helps?
All posets in P are naturally labelled. That is, for $x, y \in P$ if $x \leq y$ in $P$ then $x \leq y$ in Natural numbers. In this labelling the number of posets that satisfy the given conditions are more then one. So, I don't think that labelling is an issue here.