Not getting correct output while computing posets with some conditions.

asked 2020-11-26 06:58:57 +0200

Anonymous

I want to compute finite posets on 6 elements. Also, I want the following conditions on the posets: 2 covers 0, 4 covers 2, 3 covers 1, 5 covers 3. Also, 0, 1 are incomparable and 4, 5 are incomparable. For that I am giving the following commands:

A=[] 
P = Posets(6)
for p in P:
    if p.covers(0, 2) and p.covers(2, 4) and p.covers(1, 3) and p.covers(3, 5) and p.compare_elements(1, 0) is None and p.compare_elements(4, 5) is None:
        A.append(p);
print(A)

The output I am getting is not correct. There is only one element in sage output but that is not true. Is there any issue with my code?

Comments

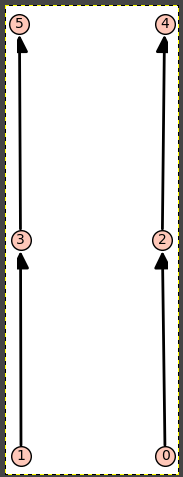
My impression is that the assumption on the element labels may be causing the unexpected result. That is, P is a list of non-isomorphic posets on 6 elements. So for each poset it contains only one possible labeling.

Perhaps iterating over all possible element labelings for each poset helps?

fidbc ( 2020-11-26 17:28:23 +0200 )edit

All posets in P are naturally labelled. That is, for $x, y \in P$ if $x \leq y$ in $P$ then $x \leq y$ in Natural numbers. In this labelling the number of posets that satisfy the given conditions are more then one. So, I don't think that labelling is an issue here.

Dharm ( 2020-11-27 05:35:49 +0200 )edit

add a comment

answered 2021-01-06 02:54:45 +0200

dan_fulea
5337 ●5 ●43 ●90

Note that ?Posets gives the following information on the functionality of this constructor, among other lines:

  The enumerated set of all posets on 3 elements, up to an
   isomorphism:

      sage: Posets(3)
      Posets containing 3 elements

The accent is put on up to isomorphism. For instance, we may miss the following poset from the list:

sage: pp = Poset(([0..5], [[0,2],[2,4],[3,5],[1,3]]))
sage: pp.show()

screenshot of some poset

Well, this poset is not exactly in this shape in P, instead we have:

sage: p0, = [p for p in P if p.is_isomorphic(pp)]
sage: p0.relations()
[[3, 3],
 [3, 4],
 [3, 5],
 [4, 4],
 [4, 5],
 [5, 5],
 [0, 0],
 [0, 1],
 [0, 2],
 [1, 1],
 [1, 2],
 [2, 2]]
sage: p0.minimal_elements()
[3, 0]
sage: pp.minimal_elements()
[1, 0]

(P has only $318$ elements, we would have more than $6!$ if the totally ordered posets would have been individually in there, instead as one representative for this isomorphism class.)

Some possibility to restrict to "interesting posets" (that may match or not the purpose) is as follows:

sage: A0 = [p for p in P if max([len(chain) for chain in p.chains()]) == 3 and len(p.minimal_elements()) == 2 and len(p.maximal_elements()) == 2]
sage: len(A0)
35

and now write some code that searches for two disjoint chains of maximal length $3$ in each $p\in A_0$...

edit flag offensive delete link

add a comment

Your Answer

Please start posting anonymously - your entry will be published after you log in or create a new account.

Not getting correct output while computing posets with some conditions.

Comments

1 Answer

Your Answer

Question Tools

Stats

Related questions

Not getting correct output while computing posets with some conditions. edit

Comments

1 Answer

Your Answer

Question Tools

Stats

Related questions

Not getting correct output while computing posets with some conditions.