integration of real functions

edit

Different algorithms lead to different expressions :

sage: f(x)=(1+sin(x))/(1-cos(x))
sage: Fm(x)=f(x).integrate(x, algorithm="maxima") ; Fm
x |--> -(cos(x) + 1)/sin(x) + log(cos(x) - 1)
sage: Fg(x)=f(x).integrate(x, algorithm="giac") ; Fg
x |--> -(2*tan(1/2*x) + 1)/tan(1/2*x) - log(tan(1/2*x)^2 + 1) + 2*log(abs(tan(1/2*x)))
sage: Fs(x)=f(x).integrate(x, algorithm="sympy") ; Fs
x |--> -1/tan(1/2*x) - log(tan(1/2*x)^2 + 1) + 2*log(tan(1/2*x))
sage: Ff(x)=f(x).integrate(x, algorithm="fricas") ; Ff
x |--> (log(-1/2*cos(x) + 1/2)*sin(x) - cos(x) - 1)/sin(x)

As you noted, the expression returned by Maxima is never real for $x\in\mathbb{R}$. This is not, by a long range, the first instance of a problematic integration result given by Maxima...

The three other expressions are real and present a pole at $x=0$.

One can check that all four expressions re-derivate to f(x) (I use Wolfram engine's FullSimplify as a shortcut) :

sage: [(h(x).diff(x)-f(x))._mathematica_().FullSimplify().sage() for h in (Fm, Fg, Fs, Ff)]
[0, -Csc(x) + Csc(conjugate(x)), 0, 0]

(The expression given for Fg is null for $x\in\mathbb{R}$).

Plotting the real function to stimulate our intuition :

sage: plot([Fm, Fg, Fs, Ff], (-1, 1), ymin=-10, ymax=10, detect_poles="show", le
....: gend_label=["Fm", "Fg", "Fs", "Ff"], axes=False, frame=True)
verbose 0 (3954: plot.py, generate_plot_points) WARNING: When plotting, failed to evaluate function at 200 points.
verbose 0 (3954: plot.py, generate_plot_points) Last error message: 'Unable to compute f(1.0)'
verbose 0 (3954: plot.py, generate_plot_points) WARNING: When plotting, failed to evaluate function at 100 points.
verbose 0 (3954: plot.py, generate_plot_points) Last error message: 'Unable to compute f(-0.007791788689424723)'
Launched png viewer for Graphics object consisting of 7 graphics primitives

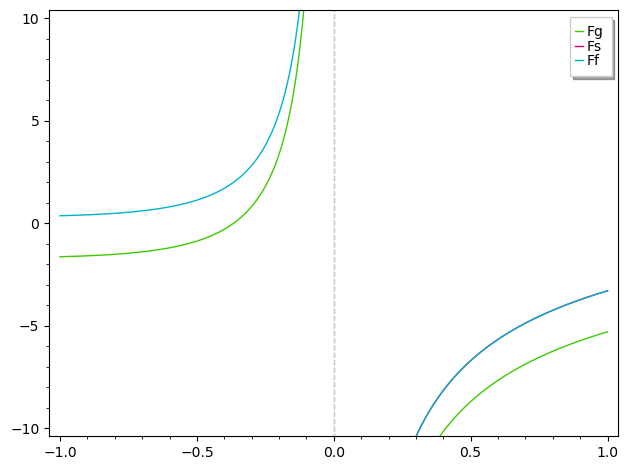
This suggests that Fs and Ff are equal and that Fg differs from them by an integration constant. I haven't been able to check this symbolically, but numerical check does not invalidate it :

sage: plot([lambda u:Fs(u)-Ff(u), lambda u:Fg(u)-Fs(u)], (-1, 1), legend_label=[
....: "Fs-Ff", "Fg-Fs"])
verbose 0 (3954: plot.py, generate_plot_points) WARNING: When plotting, failed to evaluate function at 100 points.
verbose 0 (3954: plot.py, generate_plot_points) Last error message: 'unable to simplify to float approximation'
verbose 0 (3954: plot.py, generate_plot_points) WARNING: When plotting, failed to evaluate function at 100 points.
verbose 0 (3954: plot.py, generate_plot_points) Last error message: 'unable to simplify to float approximation'
Launched png viewer for Graphics object consisting of 2 graphics primitives

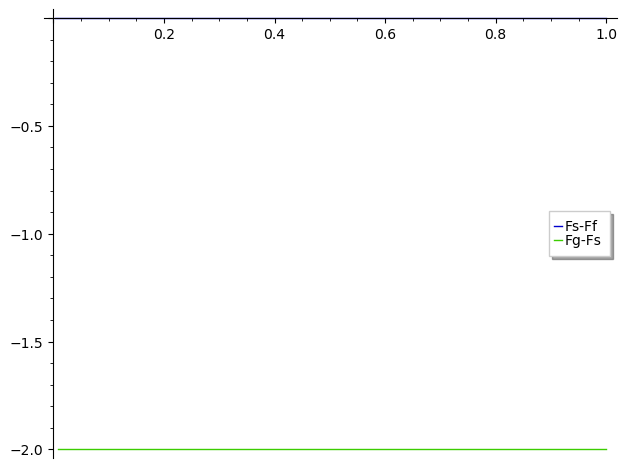
FWIW, the Wolfram engine gives yet another expression :

sage: f(x)._mathematica_().Integrate(x)
-((Sin[x/2]*(-2*Cos[x/2]*Hypergeometric2F1[-1/2, 1, 1/2, -Tan[x/2]^2] + 
    (x + 4*Log[Sin[x/2]])*Sin[x/2]))/(-1 + Cos[x]))

which (currently) does not translate automatically to Sage, but can be hand-translated :

sage: FM(x)=-((sin(x/2)(-2cos(x/2)hypergeometric([-1/2, 1],[1/2], -tan(x)^2) ....: + (x+4log(sin(x/2)))*sin(x/2)))/(cos(x)-1))

EDIT : This expression can be simplified by Wolfram engine :

sage: f(x)._mathematica_().Integrate(x).FunctionExpand().sage(locals={("Tan",1):tan})
(2*(arctan(tan(1/2*x))*tan(1/2*x) + 1)*cos(1/2*x) - (x + 4*log(sin(1/2*x)))*sin(1/2*x))*sin(1/2*x)/(cos(x) - 1)

Interestingly, one can coax Maxima to give a (partially) real result, by using the expressions of $\sin{x}$ and $\cos{x}$ in terms of $\tan{x/2}$ :

sage: Ss=(sin(2*x)==2*tan(x)/(1+tan(x)^2)).subs(x==x/2)
sage: Sc=(cos(2*x)==(1-tan(x)^2)/(1+tan(x)^2)).subs(x=x/2)
sage: # Check my distant memories
sage: bool(Ss.subs(x==2*x))
True
sage: bool(Sc.subs(x==2*x))
True
sage: f(x).subs(Ss).subs(Sc).integrate(x, algorithm="maxima")
-1/tan(1/2*x) - log(tan(1/2*x)^2 + 1) + 2*log(tan(1/2*x))

One notes that this expression is real only for $\tan{x/2}>0$.

HTH,