The problem can be approached with the following steps:
- Use nauty to generate all connected unicyclic graphs on $n$ vertices, like in my earlier answer. In each such graph:
- assign weight 1 to all edges
- find its unique cycle and iteratively assign weight $i$ to each of its edges
- use canonical labeling to eliminate duplicates
Here is a sample code:
def get_graphs(n):
S = set()
# iterate over all connected unicyclic graphs with n vertices
for G in graphs.nauty_geng(options=f'-c {n} {n}:{n}'):
# assign weight 1 to all edges of G
for e in G.edges(labels=False):
G.set_edge_label(e[0], e[1], 1)
# set of edges participating in cycles
E = set.union( *(set(c) for c in G.cycle_basis(output='edge')) )
for e in E:
# temporarily set weight of e to I
G.set_edge_label(e[0], e[1], I)
# add canonical labeling of G to set S
S.add( G.canonical_label(edge_labels=True).copy(weighted=True,immutable=True) )
# restore weight of e to 1
G.set_edge_label(e[0], e[1], 1)
return S
For example,
for H in get_graphs(4): H.show(edge_labels=True)
produces 3 graphs:
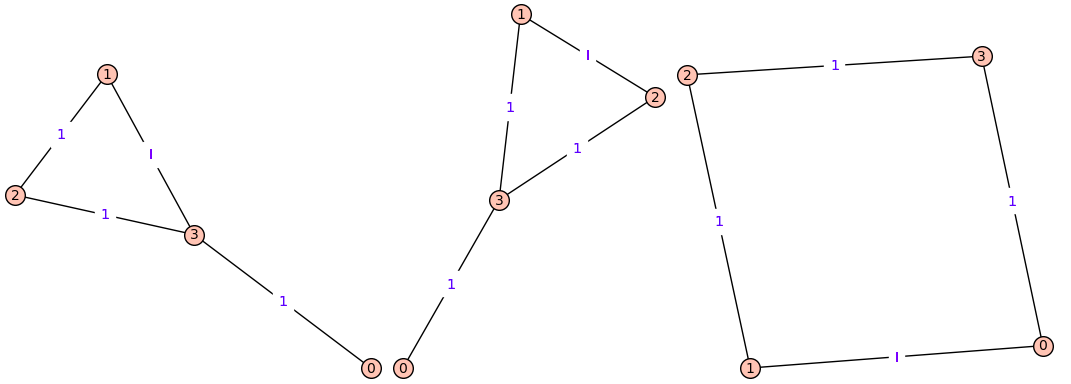
ADDED. This is how we get matrices requested in the comments (for $n=6$ as an example):
for H in get_graphs(6):
A = H.weighted_adjacency_matrix()
p = [(i,j) for i in range(A.nrows()) for j in range(i) if A[i,j]==I][0]
A[p] = -I
f = A.characteristic_polynomial()
h = f.reverse().subs({f.variables()[0]:-f.variables()[0]})
h /= h.leading_coefficient()
if f==h:
print(A,end='\n\n')
It prints the following 3 matrices:
[ 0 0 0 1 0 0]
[ 0 0 0 0 0 1]
[ 0 0 0 0 1 I]
[ 1 0 0 0 0 1]
[ 0 0 1 0 0 1]
[ 0 1 -I 1 1 0]
[ 0 0 0 0 1 0]
[ 0 0 0 1 0 0]
[ 0 0 0 0 0 1]
[ 0 1 0 0 I 1]
[ 1 0 0 -I 0 1]
[ 0 0 1 1 1 0]
[ 0 0 0 0 0 1]
[ 0 0 0 0 1 0]
[ 0 0 0 I 0 1]
[ 0 0 -I 0 0 1]
[ 0 1 0 0 0 1]
[ 1 0 1 1 1 0]
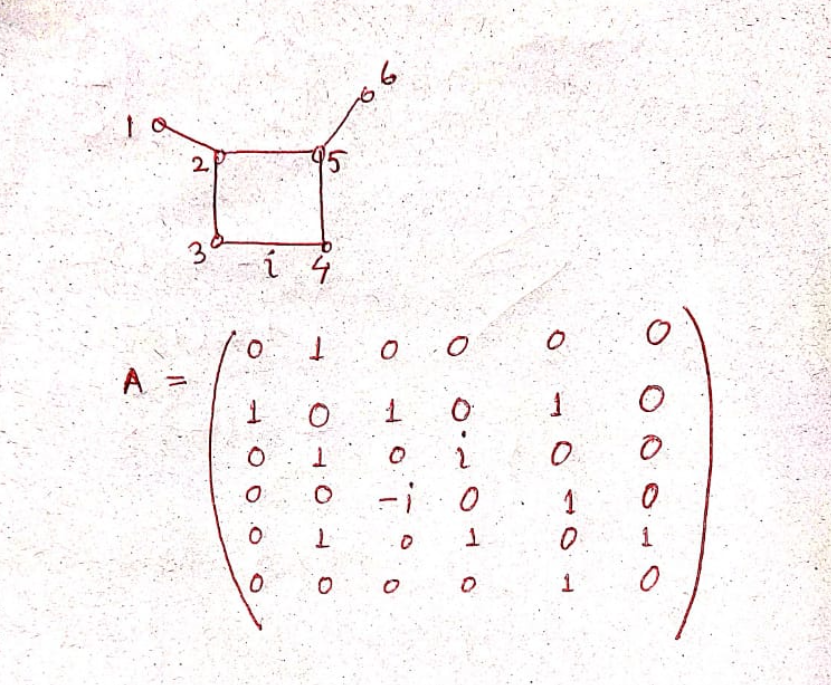



You show graph as undirected, but its adjacency matrix is not symmetric. Please clarify.
ok. actualy the graph has only one edge of weight $i$. Suppose that $[i,j]$ be the edge of weight $i$. then direction is anything, that is, one can take from i to j or from j to i. if direction is from i to j then (i,j)th entry of adjacency matrix will be $i$, and (j,i) entry is $-i$. In this case adjacency matrix will be Hermitian matrix. In the whole graph $[i,j]$ is the directed edge all other esges are non directed.
Am I clear now?