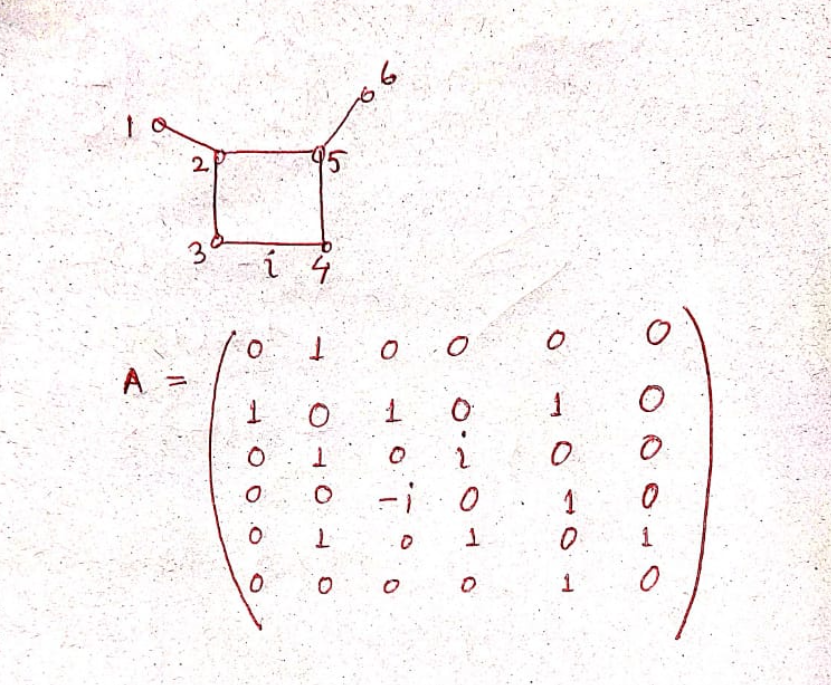How to construct the class of all connected weighted unicyclic graphs on n vertices, where exactly one edge of the cycle in the unicyclic graphs has weight i(=√−1) and remaining all the edges in the graphs are of weight 1 For example consider the following graph together with its adjacency matrix. In the adjacency matrix we take the entry (3,4) as i and (4,3) as −i, that is, just the conjugate of i
Revision history [back]
 | 1 | initial version | |
How to construct the class of all connected weighted unicyclic graphs on n vertices, where exactly one edge of the cycle in the unicyclic graphs
 | 2 | None |
How to construct the class of all connected weighted unicyclic graphs on n vertices, where exactly one edge of the cycle in the unicyclic graphs
How to construct the class of all connected weighted unicyclic graphs on n vertices, where exactly one edge of the cycle in the unicyclic graphs has weight i(=√−1) and remaining all the edges in the graphs are of weight 1 For example consider the following graph together with its adjacency matrix. In the adjacency matrix we take the entry (3,4) as i and (4,3) as −i, that is, just the conjugate of i
 | 3 | None |
How to construct the class of all connected weighted unicyclic graphs on n vertices, where exactly one edge of the cycle in the unicyclic graphs
How to construct the class of all connected weighted unicyclic graphs on n vertices, where exactly one edge of the cycle in the unicyclic graphs has weight i(=√−1) and remaining all the edges in the graphs are of weight 1 For example consider the following graph together with its adjacency matrix. In the adjacency matrix we take the entry (3,4) as i and (4,3) as −i, that is, just the conjugate of i
 | 4 | None |
How to construct the class of all connected weighted unicyclic graphs on n vertices, where exactly one edge of the cycle in the unicyclic graphs
How to construct the class of all connected weighted unicyclic graphs on n vertices, where exactly one edge of the cycle in the unicyclic graphs has weight i(=√−1) and remaining all the edges in the graphs are of weight 1 For example consider the following graph together with its adjacency matrix. In the adjacency matrix we take the entry (3,4) as i and (4,3) as −i, that is, just the conjugate of i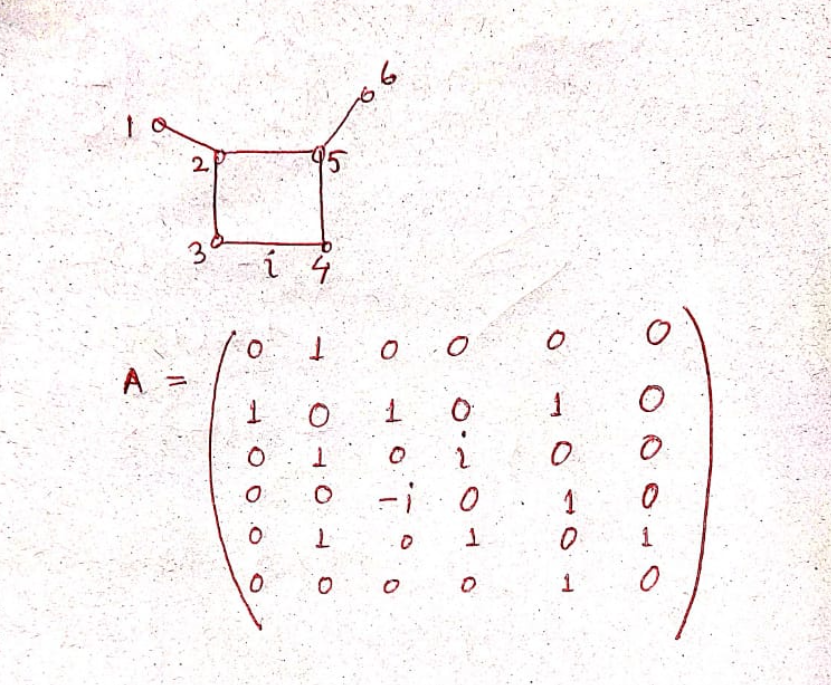
 | 5 | None |
How to construct the class of all connected weighted unicyclic graphs on n vertices, where exactly one edge of the cycle in the unicyclic graphs
How to construct the class of all connected weighted unicyclic graphs (a connected graph on n vertices is said to be unicyclic if it has n edges) on n vertices, where exactly one edge of the cycle in the unicyclic graphs has weight i(=√−1) and remaining all the edges in the graphs are of weight 1 For example consider the following graph together with its adjacency matrix. In the adjacency matrix we take the entry (3,4) as i and (4,3) as −i, that is, just the conjugate of i