differential equation
hi
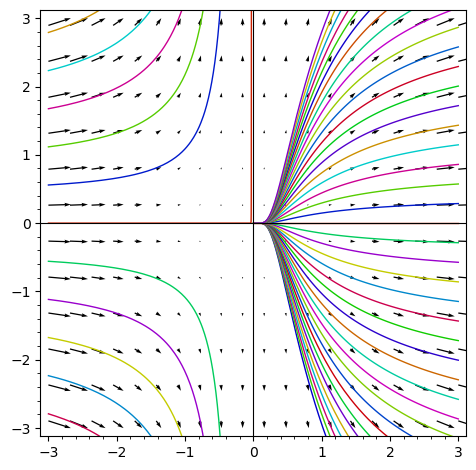
we are discovering Sagemaths and trying to solve and graph a diff equation x^2*y'=y
we tryed to agglomerate two sheets of code :
the one which solves (and works alone)
the other one which draws (and works alone)
but together they dont work (maybe because of _C ?)
any help welcome
Vinz+Erw
x = var('x'); y = function('y')
yprime=diff(y(x),x)
EqDf = (x**2)*yprime==y(x)
g(x)=desolve(EqDf, [y(x),x])
g(x)
#dessin = plot([g(x) for _C in srange(-8, 8, 0.4)], (x, -3, 3))
dessin = plot(g(x), (x, -3, 3))
y = var('y')
dessin += plot_vector_field((x^2, y), (x,-3,3), (y,-5,5))`
dessin.show(aspect_ratio = 1, ymin = -3, ymax = 3)