Hyperbolic polygons in the disc model
After noticing that there has been work towards this
(though currently stalled), we explain how exploring
the objects and their methods can suggest solutions.
Does Sage provide it already?
Progress on adapting hyperbolic polygons to other models is tracked at:
The code available in the commits posted there might cover your needs.
Regardless, let's explore a bit and build some solutions.
Exploration: an example
Let us explore a little starting from the code in the question
(thanks for providing a starting point!).
sage: DD = HyperbolicPlane().PD()
sage: lines = [DD.get_geodesic(p, q) for p, q in [(1, I), (I, -1), (-1, 1)]]
sage: p = sum(line.plot() for line in lines)
sage: p.show(figsize=3)
Launched png viewer for Graphics object consisting of 6 graphics primitives
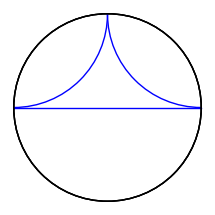
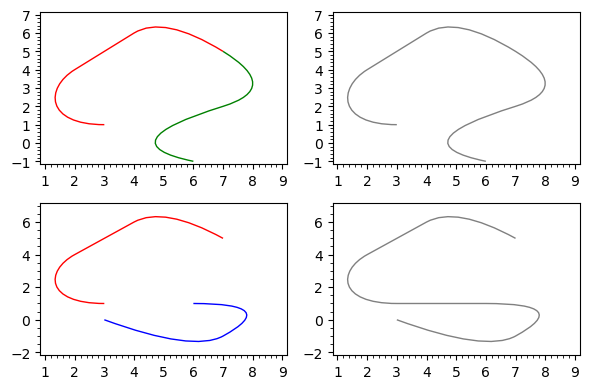
Notice that the boundary disc looks like it was plotted three times.
It is indeed the case, as we shall see. A hint, in the Sage REPL
(in the terminal) is that it mentions "6 graphics primitives",
which we can guess are the three geodesics and three copies of
the boundary circle.
To get started, let's give names to the geodesics.
sage: a, b, c = lines
Explore their methods using the TAB key: a.<TAB> reveals the method plot.
Give a name to the plots:
sage: pa, pb, pc = a.plot(), b.plot(), c.plot()
Explore their methods using the TAB key: pa.<TAB> reveals the method description.
sage: print(pa.description())
Arc with center (1.0,1.0) radii (1.0,1.0) angle 0.0
inside the sector (3.141592653589793,4.71238898038469)
Circle defined by (0.0,0.0) with r=1.0
sage: print(pb.description())
Arc with center (-1.0,1.0) radii (1.0,1.0) angle 0.0
inside the sector (-1.5707963267948966,0.0)
Circle defined by (0.0,0.0) with r=1.0
sage: print(pc.description())
Line defined by 2 points: [(-1.0, 0.0), (1.0, 0.0)]
Circle defined by (0.0,0.0) with r=1.0
We see each description consists of two lines, one for an arc
and a second one for the boundary circle. So indeed it was being
plotted three times.
Could we get rid of the boundary circle? Exploring the plot method
using a.plot? reveals the optional keyword boundary which defaults
to True. Using False instead, we can get rid of the extra circles.
sage: pa_nb = a.plot(boundary=False)
sage: pb_nb = b.plot(boundary=False)
sage: pc_nb = c.plot(boundary=False)
sage: abc0 = pa_nb + pb_nb + pc_nb # no boundary
sage: abc3 = pa + pb + pc # boundary plotted 3 times
sage: abc1 = pa_nb + pb_nb + pc # boundary plotted once
sage: abc_013 = graphics_array([abc0, abc3, abc1])
sage: abc_013.show(figsize=3)
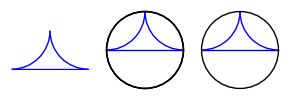
Can we get the boundary by itself? By exploring DD with DD.<TAB>,
we find a method get_background_graphic which gives it.
Besides the multiple plotting of the boundary, we observe that:
- geodesics through the origin are euclidean line segments;
their description gives their two endpoints
- geodesics not through the origin are euclidean circle arcs;
their description gives center and radius
This gives the idea of using region_plot (see the
Sage graphics tour).
For that, we write inequalities to describe the region
- inside the unit circle:
- outside the circles for sides not through the origin:
- on the appropriate side of the lines for sides through the origin:
In our case:
sage: boundary = DD.get_background_graphic()
sage: p = sum(line.plot(boundary=False) for line in lines)
sage: x, y = SR.var('x, y')
sage: ieqs = [x^2 + y^2 < 1,
....: (x - 1)^2 + (y - 1)^2 > 1,
....: (x + 1)^2 + (y - 1)^2 > 1,
....: y > 0]
sage: opt = {'incol': '#ffff7f', 'axes': False}
sage: inside = region_plot(ieqs, (x, -1, 1), (y, 0, 1), **opt)
sage: g = boundary + inside + p
sage: g.save('disc_triangle_filled_in.png', figsize=2)
sage: g.show(figsize=2)
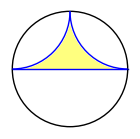
Polygon plotting function using Sage's region plot function
Based on our exploration, we write the following function:
def discgon(points, color='teal', fill_color='plum',
plot_points=65, thickness=1.5, **opt):
r"""
Return a hyperbolic polygon in the disc model as a graphics object.
INPUT:
- ``points`` -- a list of complex numbers in the unit disc,
consecutive vertices of a convex hyperbolic polygon
- ``color`` -- (default: 'teal') line thickness for sides
- ``fill_color`` -- (default: 'plum') fill color for polygon
- ``plot_points`` -- (default: 257) number of points on the arcs
- ``thickness`` -- (default: 1.5) line thickness for sides
- ``opt`` -- optional extra plotting options
EXAMPLES::
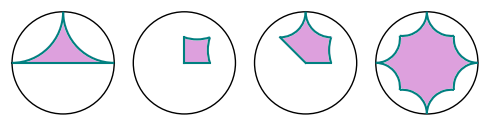
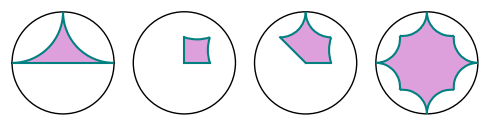
sage: a = [1, I, -1]
sage: b = [0, 1/2, 1/2 + 1/2*I, 1/2*I]
sage: c = [0, 1/2, 1/2 + 1/2*I, I, -1/2 + 1/2*I]
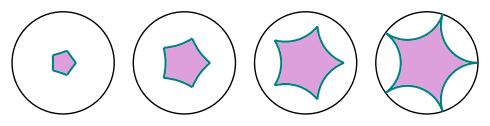
sage: d = [(3/4 if k % 2 else 1)*E(8)^k for k in range(8)]
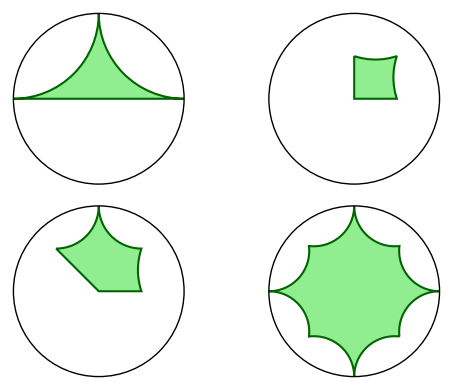
sage: abcd = graphics_array([discgon(p) for p in [a, b, c, d]])
sage: abcd.show(figsize=5)
Launched png viewer for Graphics Array of size 1 x 4
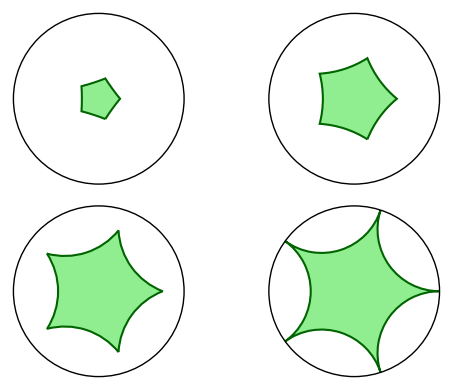
sage: fivegons = [discgon([r/4*E(5)^k for k in range(5)])
....: for r in range(1, 5)]
sage: fives = graphics_array(fivegons)
sage: fives.show(figsize=5)
Launched png viewer for Graphics Array of size 1 x 4
"""
line_opt = {'color': color, 'thickness': thickness}
fill_opt = {'incol': fill_color, 'plot_points': plot_points}
n = len(points)
if n < 3:
raise ValueError(f"need >= 3 points for polygon, got {n}")
xy = [(real(z), imag(z)) for z in points]
xx, yy = zip(*(list(z) for z in xy))
xab = min(xx), max(xx)
yab = min(yy), max(yy)
x, y = SR.var('x, y')
DD = HyperbolicPlane().PD()
relations = [x^2 + y^2 < RDF.one()]
side_plots = []
for k, q in enumerate(points, start=-1):
p = points[k]
pq = DD.get_geodesic(p, q).plot(boundary=False, **line_opt, **opt)
side_plots.append(pq)
d = pq.description()
if d.startswith('Arc'):
xc, yc, r, _ = (RDF(z) for s in d.split(')')[:-2]
for z in s.split('(')[1].split(','))
relations.append((x - xc)^2 + (y - yc)^2 > r^2)
elif d.startswith('Line'):
xa, ya, xb, yb = (RDF(z) for s in d.split(')')[:-1]
for z in s.split('(')[1].split(','))
a = yb - ya
b = xa - xb
lin_form = a * x + b * y
aff_fc = lin_form - lin_form.subs({x: p.real(), y: p.imag()})
a, r, j = max((abs(ft), ft, j)
for j, t in enumerate(xy)
for ft in [aff_fc.subs({x: t[0], y: t[1]})])
relations.append(sign(r)*aff_fc > 0)
else:
raise ValueError("unexpected side type")
inside = region_plot(relations, xab, yab, **fill_opt, **opt)
return sum(side_plots, DD.get_background_graphic(**opt) + inside)
We test our function:
sage: a = [1, I, -1]
sage: b = [0, 1/2, 1/2 + 1/2*I, 1/2*I]
sage: c = [0, 1/2, 1/2 + 1/2*I, I, -1/2 + 1/2*I]
sage: d = [(3/4 if k % 2 else 1)*E(8)^k for k in range(8)]
sage: abcd = graphics_array([discgon(p) for p in [a, b, c, d]])
sage: abcd.show(figsize=5)
Launched png viewer for Graphics Array of size 1 x 4
sage: fives = [[r/4*E(5)^k for k in range(5)] for r in range(1, 5)]
sage: fivegons = graphics_array([discgon(f) for f in fives])
sage: fivegons.show(figsize=5)
Launched png viewer for Graphics Array of size 1 x 4
Improvement ideas
The approach above is somewhat unsatisfactory for several reasons.
First, the region plot poorly fills near acute vertices,
especially if we sample too few points.
Second, sampling is wasteful in itself, since we already know
the outline of the region to plot.
This suggests approximating that outline by a euclidean polygon
and using Sage's 2D polygon plotting function, which can fill.
Replacing sides by polygonal lines is easy: sides through the origin
are already segments, and those not through the origin are circle arcs
which we can approximate by polygonal lines.
Polygon plotting function using Sage's (euclidean) 2D polygon function
Let us warm up with the initial example. The side descriptions not only
include the center and radius of the corresponding euclidean circle,
but also the two extreme angles for the arc.
So we can write something like:
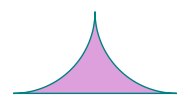
sage: nsteps = 64
sage: s, t = (3.141592653589793, 4.71238898038469)
sage: step = (t - s) / nsteps
sage: stop = s - step / 2
sage: aa = [(1 + cos(x), 1 + sin(x)) for x in srange(t, stop, -step)]
sage: s, t = (-1.5707963267948966, 0.0)
sage: step = (t - s) / nsteps
sage: stop = s - step / 2
sage: bb = [(-1 + cos(x), 1 + sin(x)) for x in srange(t, stop, -step)]
sage: cc = [(-1.0, 0.0), (1.0, 0.0)]
sage: abc = aa + bb + cc
sage: abc_gon = polygon2d(abc, color='plum', edgecolor='teal', axes=False)
sage: abc_gon.show(figsize=2)
Turning this into a function, we get:
def disc_ngon(points, color='teal', fill_color='plum',
thickness=1.5, nsteps=256, **opt):
r"""
Return a hyperbolic polygon in the disc model as a graphics object.
INPUT:
- ``points`` -- list of complex numbers in the unit disc for vertices
of a convex hyperbolic polygon listed counterclockwise
- ``color`` -- (default: 'teal') the line color for the sides
- ``fill_color`` -- (default: 'plum') the fill color for the polygon
- ``thickness`` -- (default: 1.5) the line thickness for the sides
- ``nsteps`` -- (default: 256) number of steps for circular sides
- ``opt`` -- optional extra options
Circular sides are turned into polygonal lines with ``nsteps`` segments
for filling the polygon.
EXAMPLES::
sage: a = [1, I, -1]
sage: b = [0, 1/2, 1/2 + 1/2*I, 1/2*I]
sage: c = [0, 1/2, 1/2 + 1/2*I, I, -1/2 + 1/2*I]
sage: d = [(3/4 if k % 2 else 1)*E(8)^k for k in range(8)]
sage: abcd = graphics_array([discgon(p) for p in [a, b, c, d]])
sage: abcd.show(figsize=5)
Launched png viewer for Graphics Array of size 1 x 4
sage: fivegons = [discgon([r/4*E(5)^k for k in range(5)])
....: for r in range(1, 5)]
sage: fives = graphics_array(fivegons)
sage: fives.show(figsize=5)
Launched png viewer for Graphics Array of size 1 x 4
"""
line_opt = {'color': color, 'thickness': thickness}
fill_opt = {'color': fill_color, 'thickness': 0}
n = len(points)
if n < 3:
raise ValueError(f"need >= 3 points for polygon, got {n}")
xy = [(real(z), imag(z)) for z in points]
DD = HyperbolicPlane().PD()
side_plots = []
vertices = []
for k, q in enumerate(points, start=-1):
p = points[k]
vertices.append(xy[k])
pq = DD.get_geodesic(p, q).plot(boundary=False, **line_opt, **opt)
side_plots.append(pq)
d = pq.description()
if d.startswith('Arc'):
xc, yc, r, _, s, t = (RDF(z) for s in d.split(')')[:-1]
for z in s.split('(')[1].split(','))
step = (t - s) / nsteps
vertices.extend([(xc + r*cos(x), yc + r*sin(x))
for x in srange(t + step/2, s, -step)])
inside = polygon2d(vertices, **fill_opt, **opt)
return sum(side_plots, DD.get_background_graphic(**opt) + inside)
We test our function:
sage: a = [1, I, -1]
sage: b = [0, 1/2, 1/2 + 1/2*I, 1/2*I]
sage: c = [0, 1/2, 1/2 + 1/2*I, I, -1/2 + 1/2*I]
sage: d = [(3/4 if k % 2 else 1)*E(8)^k for k in range(8)]
sage: abcd = graphics_array([disc_ngon(p) for p in [a, b, c, d]])
sage: abcd.show(figsize=5)
Launched png viewer for Graphics Array of size 1 x 4
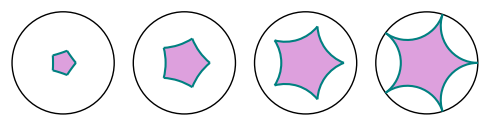
sage: fives = [[r/4*E(5)^k for k in range(5)] for r in range(1, 5)]
sage: fivegons = graphics_array([disc_ngon(f) for f in fives])
sage: fivegons.show(figsize=5)
Launched png viewer for Graphics Array of size 1 x 4











There is hyperbolic_polygon, but alas only for the upper half-space, I think..
Sorry for taking so long to post a somewhat satisfactory answer.
Probably my initial answer (just pointing to the corresponding ticket) should have been a comment instead, so that, seeing the question unanswered, more people might have given it a shot.
I hope the functions in my answer are at least a step towards your needs.
I saw you posted a follow-up question on concatenating Bézier paths and filling a path made of Bézier paths.
The same idea crossed my mind while composing my answer to the present question!