A polyhedron little problem
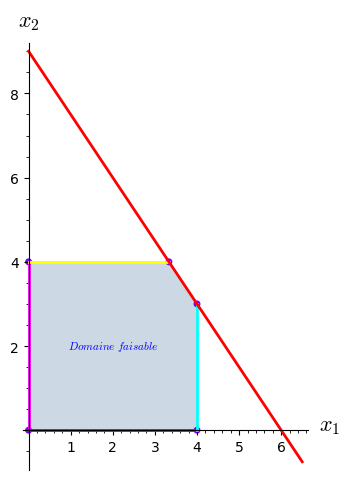
I do not know if I make a mistake On the following problem. I have the polygon
var('x_1') # toute variable utilisée doit être préalablement définie
p1 = plot((9 - (3/2)*x_1),(x_1,0,6.5),color='red',axes_labels=['$x_1$','$x_2$'], thickness=2,zorder=2)
l0 = line([(0,0),(0,4)],color='magenta', thickness=2)
l1 = line([(0,4),(10/3,4)],color='yellow', thickness=2)
l2 = line([(0,0),(4,0)],color='green', thickness=2)
l3 = line([(4,0),(4,3)],color='cyan', thickness=2)
c1=point((0,0),pointsize=25, rgbcolor=hue(0.75),aspect_ratio='automatic',zorder=1)
c2=point((0,4),pointsize=25, rgbcolor=hue(0.75),aspect_ratio='automatic',zorder=1)
c3=point((4,0),pointsize=25, rgbcolor=hue(0.75),aspect_ratio='automatic',zorder=1)
c4=point((10/3,4),pointsize=25, rgbcolor=hue(0.75),aspect_ratio='automatic',zorder=1)
c5=point((4,3),pointsize=25, rgbcolor=hue(0.75),aspect_ratio='automatic',zorder=1)
pol=polygon([(0,0),(0,4),(10/3,4),(4,3),(4,0)],rgbcolor=(0.025,0.25,0.5),alpha=0.2)
D=text(r"$Domaine\,\, faisable$",(2,2),fontsize=8)
show(pol+l0+l1+l2+l3+p1+c1+c2+c3+c4+c5+D)
( Incidently I am oblige to plot an horizontal line through line not as an equality. Is there an other way ?) Now if I ask directly to plot the polygon by
var('x_1') # toute variable utilisée doit être préalablement définie
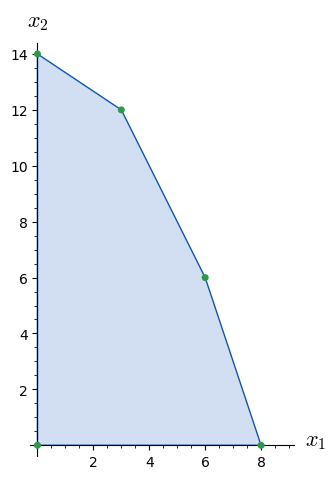
pol1=Polyhedron(ieqs=[(18,-2,-1),(42,-2,-3),(24,-3,-1),(0,1,0),(0,0,1)])
S=[s for s in pol1.Vrepresentation()]
SS=[(S[i][0],S[i][1]) for i in range(len(S))]
C = [circle(SS[i],.1,fill=True,edgecolor='#2f974a',facecolor='#2f974a') for i in range(len(SS))]
PC = [plot(C[i])for i in range(len(SS))]
gon=polygon(SS,fill=True,color='#d2def1',edgecolor="#0e56ad")
lab=plot(0,(x,0,9), color='black',axes_labels=['$x_1$','$x_2$'],thickness=0.0001)#ligne fictive d'où l'épaisseur pour obtenir les labels des axes
I obtain a simple rectangle which is not the case. show(lab+gon+sum(PC[i] for i in range(len(SS))))