Revision history [back]

This is more a comment than an answer, posted as an answer since it is too long to fit in a comment.

I do not observe (or do not understand) the problem (on macOS with Sage 9.2.beta12 built from source).

Below a slightly rewritten form of the code from the question, with pictures. (The original code gives me the same pictures.)

• If you get the same pictures, say what the problem is with them.
• If not, upload yours and say what version of Sage you are using.

If posting an image on Ask Sage is too tedious, there are various other ways to do that:

• put the code on SageCell, get a link and post it here
• put the code on CoCalc, share it, post the link here
• upload a Jupyter worksheet somewhere, link to it here

Below I am adding sectioning to make it easy to ask any question relating to a specific part of my answer (or the corresponding part in the question).

0.

0.0.

Define graphic options for the various graphics objects.

sage: options_plot = {'axes_labels': ['$x_1$','$x_2$'], 'thickness': 2, 'zorder': 2}
sage: options_line = {'thickness': 2}
sage: options_point = {'pointsize': 25, 'rgbcolor': hue(0.75),
....:                  'aspect_ratio': 'automatic', 'zorder': 1}
sage: options_pol = {'rgbcolor': (0.025, 0.25, 0.5), 'alpha': 0.2}

0.1.

A function and its plot.

sage: f1 = lambda x: 9 - (3/2)*x
sage: p1 = plot(f1, (0, 6.5), color='red', **options_plot)

0.2.

Four lines.

sage: l0 = line([(0, 0), (0, 4)], color='magenta', **options_line)
sage: l1 = line([(0, 4), (10/3, 4)], color='yellow', **options_line)
sage: l2 = line([(0, 0), (4, 0)], color='green', **options_line)
sage: l3 = line([(4, 0), (4, 3)], color='cyan', **options_line)

0.3.

Five corners.

sage: c1 = point((0, 0), **options_point)
sage: c2 = point((0, 4), **options_point)
sage: c3 = point((4, 0), **options_point)
sage: c4 = point((10/3, 4), **options_point)
sage: c5 = point((4, 3), **options_point)

0.4.

One polygon.

sage: pol = polygon([(0, 0), (0, 4), (10/3, 4), (4, 3), (4, 0)], **options_pol)

0.5.

A text description, and a graphics with all these elements.

sage: D = text(r"$Domaine\,\, faisable$", (2, 2), fontsize=8)
sage: G = sum([pol, l0, l1, l2, l3, p1, c1, c2, c3, c4, c5], D)

0.6

Save the picture to a file.

sage: G.save('ask_53468_G.png')

0.7.

Show the whole picture.

sage: G.show()
Launched png viewer for Graphics object consisting of 12 graphics primitives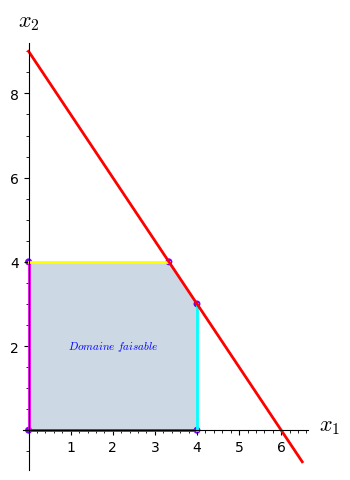

1.

1.0.

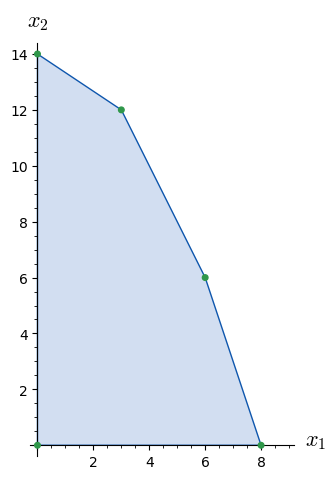
A list of inequalities and the corresponding polygon.

sage: ieqs1 = [(18, -2, -1), (42, -2, -3), (24, -3, -1), (0, 1, 0), (0, 0, 1)]
sage: pol1 = Polyhedron(ieqs=ieqs1)

1.1.

Turn the polygon vertices into tuples.

sage: S = [s for s in pol1.Vrepresentation()]
sage: SS = [tuple(s) for s in S]

1.2.

Small circles around the vertices.

sage: options_circle = {'fill': True, 'edgecolor': '#2f974a', 'facecolor': '#2f974a'}
sage: C = [circle(s, .1, **options_circle) for s in SS]
sage: PC = [plot(c) for c in C]

1.3.

The polygon as a graphics object.

sage: gon = polygon(SS, fill=True, color='#d2def1', edgecolor="#0e56ad")

1.4.

The constant zero function and its plot.

sage: z = lambda x: 0
sage: lab = plot(z, (0, 9), color='black', axes_labels=['$x_1$', '$x_2$'], thickness=0.0001)

1.5.

Everything in one graphics object.

sage: GG = sum(PC, lab + gon)

1.6.

Save the picture.

sage: GG.save('ask_53468_GG.png')

1.7.

Show the whole picture.

sage: GG.show()
Launched png viewer for Graphics object consisting of 7 graphics primitives