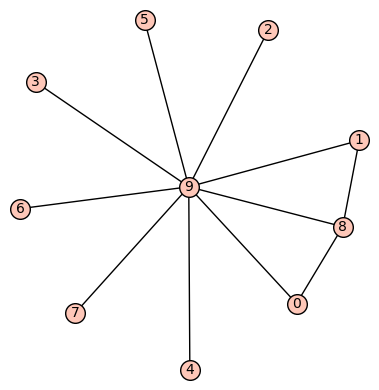
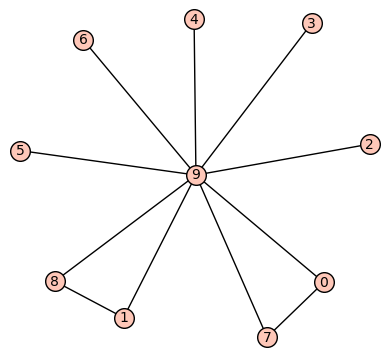
How to obtain the graph having highest algebraic connectivity?
for G in graphs.nauty_geng("10-c"):
if G.size()==11:
L = G.laplacian_matrix().eigenvalues()
L.sort()
show(L)
G.show()
Using this code I have obtained the connected graphs on 10 vertices with 11 edges. Also I have obtained the Laplacian eigenvalues also for the corresponding graphs. The second smallest eigenvalue of Laplacian matrix is called the algebraic connectivity. Now among all these graphs, I need those graphs which have highest algebraic connectivity among all the graphs on 10 vertices with 11 edges. How we can do that?