Problem with implicit_plot
I have three huge degree 31 bivariate polynomials (20,000 characters long each) I want to plot, but I keep getting a lot of noise in my plot. I can't upload it, but the point is that in some regions I just get colorful noise. I've tried defining the polynomials over RealField(n) and increasing the number of plot_points, but neither of these approaches work. Any ideas on how to work around this? Thanks.
Edit: Tried using sympy's plot_implicit and it's so (SO!) slow. Then used numpy's contour_plot and it's fast, but has the same problem as sage.
Here's the code that produces the polynomials and plot. Be patient as it could be a bit slow (depending on your machine).
plot = Graphics()
m = 32-1
D = [(i,j) for i in range(0,m+1) for j in range(0,m+1) if i+j<m+1]
#Polygon
P = Polyhedron( vertices= [(0, 0), (32, 44), (23, 0), (10, 14), (2, 3)] )
points = P.integral_points()
plot_pts = point(points, rgbcolor=(0, 0, 0), size = 20).plot()
plot_np = P.plot(fill = False, point=False, line='black')
M = matrix(ZZ, len(points), len(D), 0)
for row_num, row in enumerate(points):
for col_num, column in enumerate(D):
i, j = row
a, b= column
#Matrix for interpolation:
M[row_num, col_num] = (i^a)*(j^b)
R = PolynomialRing(QQ, 2, 'xy')
S = PolynomialRing(RealField(500), 2, 'uv')
x, y = R.gens()
u, v = S.gens()
K = M.right_kernel()
Kdim = K.dimension()
print(Kdim)
if Kdim > 0:
for l in range(Kdim):
K_basis = K.basis()[l]
#Writing the interpolating polynomial
f=0
for order, bidegree in enumerate(D):
a, b = bidegree
f += list(K_basis)[order] * u^a * v^b
F = f.factor()
f = F[6][0]
cols = ['red', 'blue', 'green']
interpolation = implicit_plot(f, (u,-1,34), (v,-1,45), plot_points=100, color=cols[l])
plot += interpolation
plot += plot_pts + plot_np
plot.show(figsize=10)
Edit 2: Using the mpmath library in Python and with the aid of Sébastien's code below I wrote a routine that allows us to control the root finding method and precision of our computations. I tried several methods, secant (default), newton, hailley, mnewton, etc. without success. Changing the precision and tolerance of the root finding function from mpmath didn't help either. I think this polynomial just behaves too wildly in the region of the plot.
Here's the code and relevant documentation for the "mpmath.findroot" function:
http://mpmath.org/doc/current/calculu... :
from sympy import *
import matplotlib.pyplot as plt
import mpmath as mp
mp.dps = 100
stepx = 0.1
stepy = 0.5
xrange = np.arange(7.5,12.5, stepx)
yrange = np.arange(0, 5, stepy)
def plot_roots_of_f(f):
L = []
for u in xrange:
for v in yrange:
Root = mp.findroot(f.eval({x:u}),v, method = 'mnewton', tol = E-60, verbose=False,verify=False)
L.append([u,Root])
return plt.plot(*zip(*L),linestyle='None', marker='.')
plot_roots_of_f(f)
plt.show()

Could you please try to upload the code somewhere so taht we can give a try ?
I added the code, @tmonteil
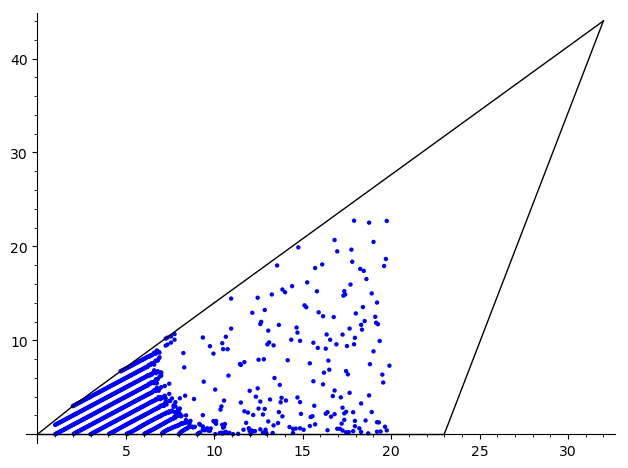
The code runs in few seconds on my machine (does not seem computationally heavy?). The output is the overlay the three implicit plot which indeed looks like "colorful noise". But what is the expected result? Is the equation
f==0suppose to pass through all of the integer points inside the polygon?@Sébastien exactly. These three polynomials should define nice graphs passing through said points.This must be the case because for each fixed value of x there can be at most 31 values of y in the plot. These vary continuously as x does, so there's just no way it looks as the plot suggests. In my case this is very clear for x<10, where the plot looks well. The issue happens further away from the origin.
I think the generic
implicit_plotfunction is no good for your functionfwhich involves sums of large numbers (possibly done with using float inputs) that must equal to zero at the end. I would suggest you to write your own drawing function based on factorization of the univariate polynomialfafter evaluation at specific values ofu. For example: