Confusion about integrating a string.
sagemath 8.9
Follow up based on answer here why-sagemath-can-integrate-a-string sagemath can integrate a string.
Well. Sometimes it can, and sometimes it does not. And this getting confusing. For example
sage: integrate("ln(t)",t,algorithm="fricas")
integral(ln(t), t)
But if it is not a string, it works.
sage: integrate(ln(t),t,algorithm="fricas")
t*log(t) - t
But using "log(t)" as string, instead of "ln(t)" now it works
sage: integrate("log(t)",t,algorithm="fricas")
t*log(t) - t
Adding SR makes no difference
sage: integrate(SR("ln(t)"),t,algorithm="fricas")
integral(ln(t), t)
sage: integrate(SR("log(t)"),t,algorithm="fricas")
t*log(t) - t
sage:
Why does it fail when doing "ln(t)" but it works with "log(t)" ? I am sure there is a good reason.
And sometimes it crashes also
sage: integrate("ln(1-t)",t,algorithm="fricas")
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-24-c1ae517e9ade> in <module>()
----> 1 integrate("ln(1-t)",t,algorithm="fricas")
/usr/lib/python2.7/site-packages/sage/misc/functional.pyc in integral(x, *args, **kwds)
754 else:
755 from sage.symbolic.ring import SR
--> 756 return SR(x).integral(*args, **kwds)
757
758
/usr/lib/python2.7/site-packages/sage/symbolic/expression.pyx in sage.symbolic.expression.Expression.integral (build/cythonized/sage/symbolic/expression.cpp:64032)()
12360 R = ring.SR
12361 return R(integral(f, v, a, b, **kwds))
> 12362 return integral(self, *args, **kwds)
12363
12364 integrate = integral
/usr/lib/python2.7/site-packages/sage/symbolic/integration/integral.pyc in integrate(expression, v, a, b, algorithm, hold)
910 if not integrator:
911 raise ValueError("Unknown algorithm: %s" % algorithm)
--> 912 return integrator(expression, v, a, b)
913 if a is None:
914 return indefinite_integral(expression, v, hold=hold)
/usr/lib/python2.7/site-packages/sage/symbolic/integration/external.pyc in fricas_integrator(expression, v, a, b, noPole)
381
382 from sage.interfaces.fricas import fricas
--> 383 ex = fricas(expression)
384
385 if a is None:
/usr/lib/python2.7/site-packages/sage/interfaces/interface.pyc in __call__(self, x, name)
293 # user-assigned name might change its value, so we return a
294 # new element.
--> 295 result = self._coerce_from_special_method(x)
296 return result if name is None else result.name(new_name=name)
297 except TypeError:
/usr/lib/python2.7/site-packages/sage/interfaces/interface.pyc in _coerce_from_special_method(self, x)
321 s = '_gp_'
322 try:
--> 323 return (x.__getattribute__(s))(self)
324 except AttributeError:
325 return self(x._interface_init_())
/usr/lib/python2.7/site-packages/sage/structure/sage_object.pyx in sage.structure.sage_object.SageObject._fricas_ (build/cythonized/sage/structure/sage_object.c:7272)()
744 import sage.interfaces.fricas
745 G = sage.interfaces.fricas.fricas
--> 746 return self._interface_(G)
747
748 def _fricas_init_(self):
/usr/lib/python2.7/site-packages/sage/symbolic/expression.pyx in sage.symbolic.expression.Expression._interface_ (build/cythonized/sage/symbolic/expression.cpp:7633)()
797 if is_a_constant(self._gobj):
798 return self.pyobject()._interface_(I)
--> 799 return super(Expression, self)._interface_(I)
800
801 def _maxima_(self, session=None):
/usr/lib/python2.7/site-packages/sage/structure/sage_object.pyx in sage.structure.sage_object.SageObject._interface_ (build/cythonized/sage/structure/sage_object.c:5474)()
667 except Exception:
668 raise NotImplementedError("coercion of object %s to %s not implemented:\n%s\n%s" % (repr(self), I))
--> 669 X = I(s)
670 if c:
671 try:
/usr/lib/python2.7/site-packages/sage/interfaces/interface.pyc in __call__(self, x, name)
286
287 if isinstance(x, string_types):
--> 288 return cls(self, x, name=name)
289 try:
290 # Special methods do not and should not have an option to
/usr/lib/python2.7/site-packages/sage/interfaces/expect.pyc in __init__(self, parent, value, is_name, name)
1474 except (RuntimeError, ValueError) as x:
1475 self._session_number = -1
-> 1476 raise_(TypeError, TypeError(*x.args), sys.exc_info()[2])
1477 except BaseException:
1478 self._session_number = -1
/usr/lib/python2.7/site-packages/sage/interfaces/expect.pyc in __init__(self, parent, value, is_name, name)
1469 else:
1470 try:
-> 1471 self._name = parent._create(value, name=name)
1472 # Convert ValueError and RuntimeError to TypeError for
1473 # coercion to work properly.
/usr/lib/python2.7/site-packages/sage/interfaces/interface.pyc in _create(self, value, name)
489 def _create(self, value, name=None):
490 name = self._next_var_name() if name is None else name
--> 491 self.set(name, value)
492 return name
493
/usr/lib/python2.7/site-packages/sage/interfaces/fricas.pyc in set(self, var, value)
588 cmd = '%s%s%s;' % (var, self._assign_symbol(), value)
589 output = self.eval(cmd, reformat=False)
--> 590 self._check_errors(value, output)
591
592 def get(self, var):
/usr/lib/python2.7/site-packages/sage/interfaces/fricas.pyc in _check_errors(self, line, output)
562 for old, new in replacements:
563 output = output.replace(old, new)
--> 564 raise RuntimeError("An error occurred when FriCAS evaluated '%s':\n%s" % (line, output))
565
566 # or even an error
TypeError: An error occurred when FriCAS evaluated 'operator("ln")(((t)*(-1))+(1))':
There are 1 exposed and 1 unexposed library operations named elt having
1 argument(s) but none was determined to be applicable. Use HyperDoc
Browse, or issue
)display op elt
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find application of object of type BasicOperator to argument(s)
of type(s)
Polynomial(Integer)
But OK if not a string
sage: integrate(ln(1-t),t,algorithm="fricas")
(t - 1)*log(-t + 1) - t
ps. The whole idea of allowing a string as input to integrate is not right IMHO, but I assume it is allowed for a good reason. If it is to be allowed, it should be treated as a constant with no interpretation at all. This is what Mathematica does:
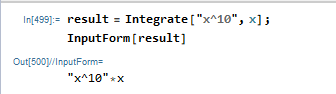
But I think Maple handles this best by rejecting a string all together
int("x^10",x)
Error, (in int) wrong number (or type) of arguments: wrong type of integrand passed to indefinite integration.
Another observation: This seems to affect fricas and maxima, but not giac
sage: integrate("ln(t)",t,algorithm="fricas")
integral(ln(t), t)
sage: integrate("ln(t)",t,algorithm="giac")
t*log(t) - t
sage: integrate("ln(t)",t,algorithm="maxima")
integrate(ln(t), t)
Thank you --Nasser
