tree of vectors
This is a more complicated version of apply functions iteratively
I have a starting "seed" vector, say
e1 = matrix(4,1,(1,0,0,0))
Next, I have a collection of 4x4 matrices
thin_group = [T1,T2,T3,T4,T5]
where
$T1 = \left(\begin{array}{rrrr} -1 & 0 & 0 & 0 \\ 2 & 1 & 0 & 0 \\ 4 & 0 & 1 & 0 \\ 4 & 0 & 0 & 1 \end{array}\right), T2 = \left(\begin{array}{rrrr} 1 & 2 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 4 & 1 & 0 \\ 0 & 4 & 0 & 1 \end{array}\right), T3 = \left(\begin{array}{rrrr} 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right), T4 = \left(\begin{array}{rrrr} 1 & 6 & 0 & 6 \\ 0 & 3 & 0 & 2 \\ 0 & 4 & 1 & 4 \\ 0 & -4 & 0 & -3 \end{array}\right), T5 = \left(\begin{array}{rrrr} 3 & 0 & 0 & 2 \\ 6 & 1 & 0 & 6 \\ 4 & 0 & 1 & 4 \\ -4 & 0 & 0 & -3 \end{array}\right)$
These matrices either fix e1 or send to a different vector. I have a "height" function, which just measures how large the vector entries are getting.
def h(X):
return max(abs(X[0,0],abs(X[1,0]), abs(X[2,0]),abs(X[3,0]))
I want to develop the following procedure:
hmax = 50
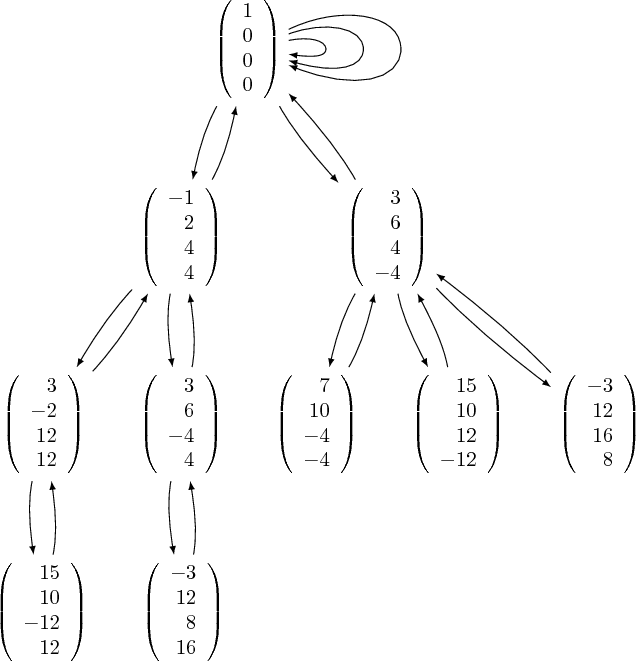
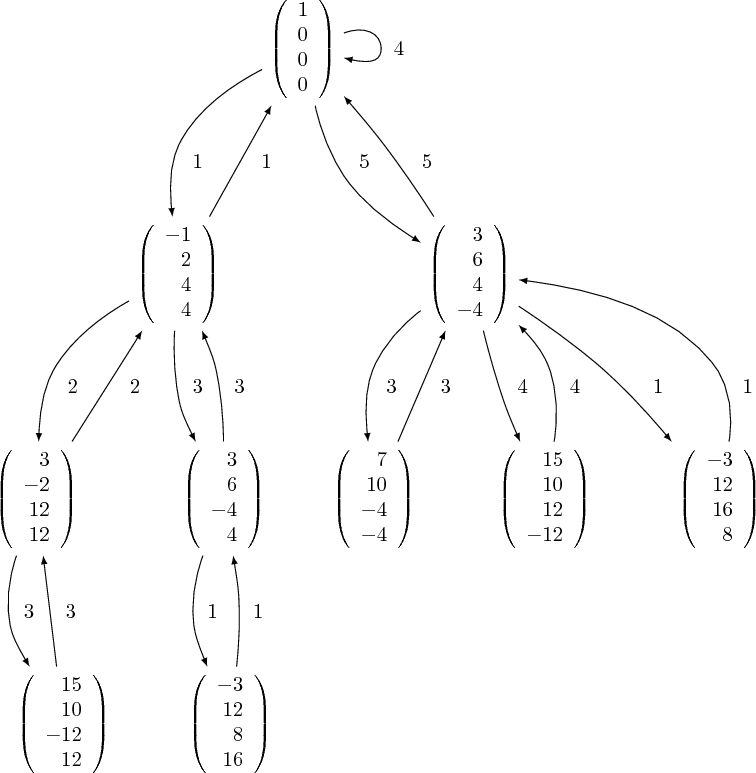
Begin applying T1,...,T5 to e1. As soon as I get a different vector (T1*e1 = (-1,2,4,4)), measure the height of that vector. If the height is below hmax (h(-1,2,4,4) = 4 < hmax = 50), store that vector somewhere. Now apply another matrix from thin_group to (-1,2,4,4), (but not T1 again). If the new vector has a height below hmax, store it, and apply another matrix from thin_group, just not the previous one. Continue this process until we reach a vector with a height larger than hmax. Once this happens, go back to the previous vector and apply a different matrix from thin_group i.e. go up a different branch of the tree. Go up this branch until hmax is exceeded, then go up a different branch, etc.. Eventually, this process will generate all thin_group images of e1 with hmax < 50. (this is probably about 50,000 vectors)
This procedure should "remember" the vectors that were counted/stored, so I'm thinking that I may be able to index each vector in the tree with a sequence (a1,a2,a3,...,an) where aj=1,2,3,4,5 to denote which matrix T1,...,T5 we applied previously.
Any/all ideas or partial solutions greatly appreciated. Thanks!