Fast plots - How do I do those?

asked 2015-08-21 00:06:40 +0100

Peter Luschny
548 ●14 ●37 ●58

I have no experience with Sage plots so I think I make something wrong. With Maple

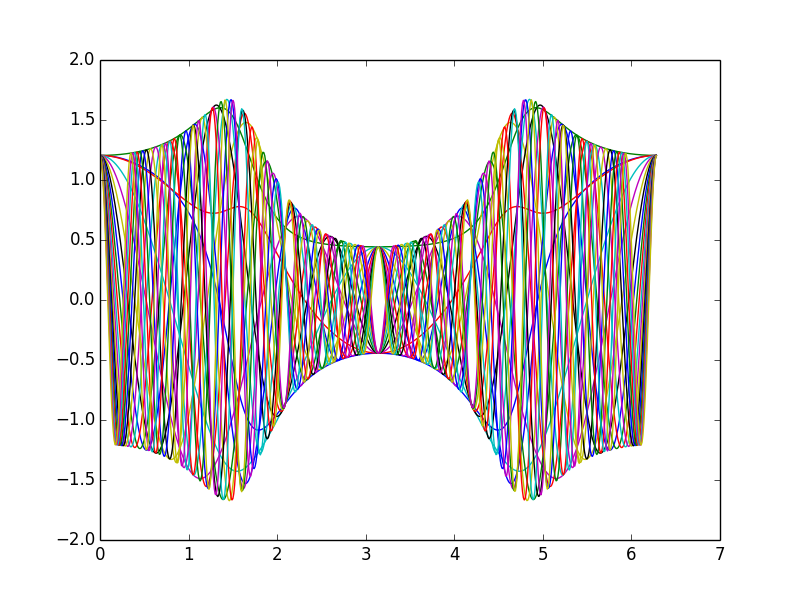
plot([seq(Re(exp(I*t*(1-n))*(1+(exp(exp(I*t))-1)/(exp(2*exp(I*t))+1))),n=1..20)],t=0..2*Pi);

takes less than 1 second and it looks perfect.

With Sage (executed at SMC)

f = lambda x,n: (exp(i*x*(1-n))*(1+(exp(exp(i*x))-1)/(exp(2*exp(i*x))+1))).real()
bat = plot(f(x,0), (0,2*pi), color=Color(0,0,0), ymin=-1.6, ymax=1.6)
for n in sxrange(1,20,1):
    bat += plot(f(x,n), (0,2*pi), rgbcolor=(n/2,n/5,n/3), ymin=-1.6, ymax=1.6)
bat

takes longer than the lifespan of Methuselah. How can I speed things up?

answered 2015-08-21 20:55:36 +0100

fidbc

2423 ●4 ●26 ●61

A possibility would be to use matplotlib+numpy. For example:

import numpy as np
import matplotlib.pyplot as plt

def get_f( n ):
    i=np.complex(0,1)
    def func(t):
        return np.exp(i*t*(1-n))*(1+(np.exp(np.exp(i*t))-1)/(np.exp(2*np.exp(i*t))+1))
    return func

def mat_plot():
    t = np.arange(0.,2*np.pi,0.01)
    for i in range(20):
        func = get_f(i)
        ft = func(t)
        plt.plot(t,np.real(ft))
    plt.show()
    plt.clf()

Takes only 0.5s at SMC (and 234ms on my laptop). Sample output:

image description

edit flag offensive delete link

Comments

Excellent, thanks! I call this plot Bernoulli's batman. If you want to know why you can go here: http://luschny.de/math/zeta/Bernoulli...

Peter Luschny ( 2015-08-21 21:27:28 +0100 )edit

@Peter Luschny Nice! Are you planning on translating the source on the appendix to Sagemath?

fidbc ( 2015-08-22 23:21:26 +0100 )edit

Yes, I will add also a Sage version and add your graphic script, if you allow. The page is still under construction and more things might come.

Peter Luschny ( 2015-08-24 19:52:55 +0100 )edit

As long as it preserves the same CC license I'm fine. I'll try to tweak the code a bit more.

fidbc ( 2015-08-26 01:52:15 +0100 )edit

add a comment

Your Answer

Please start posting anonymously - your entry will be published after you log in or create a new account.

Fast plots - How do I do those?

1 Answer

Comments

Your Answer

Question Tools

Stats

Related questions

Fast plots - How do I do those? edit

1 Answer

Comments

Your Answer

Question Tools

Stats

Related questions

Fast plots - How do I do those?