call graph of a recursive function
A colleague asked if I could write some code to show the call graph of a recursive function. I came up with this:
def grafo_llamadas(f):
class G(object):
def __init__(self, f):
self.f=f
self.stack = []
self.g = DiGraph()
def __call__(self, *args):
if self.stack:
sargs = ','.join(str(a) for a in args)
last = ','.join(str(a) for a in self.stack[-1])
if self.g.has_edge(last, sargs):
l = self.g.edge_label(last, sargs)
self.g.set_edge_label(last, sargs, l + 1)
else:
self.g.add_edge(last, sargs, 1)
else:
self.g = DiGraph()
self.stack.append(args)
v = self.f(*args)
self.stack.pop()
return v
def grafo(self):
return self.g
return G(f)
@grafo_llamadas
def fibo(n):
if n<=2:
return 1
else:
return fibo(n-1) + fibo(n-2)
fibo(6)
g = fibo.grafo()
g.show(edge_labels=True)
@grafo_llamadas
def particiones(n, k):
if k == n:
return [[1]*n]
if k == 1:
return [[n]]
if not(0 < k < n):
return []
ls1 = [p+[1] for p in particiones(n-1, k-1)]
ls2 = [[parte+1 for parte in p] for p in particiones(n-k, k)]
return ls1 + ls2
particiones(8,3)
g = particiones.grafo()
g.show(edge_labels=True, figsize=(8,8), vertex_size=500)
Do you like it? Can you improve it?
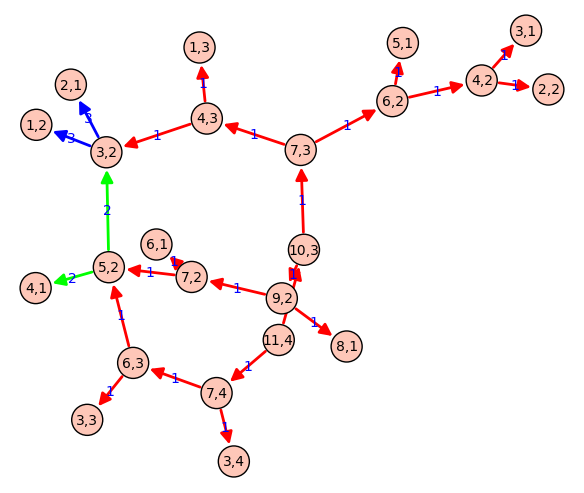
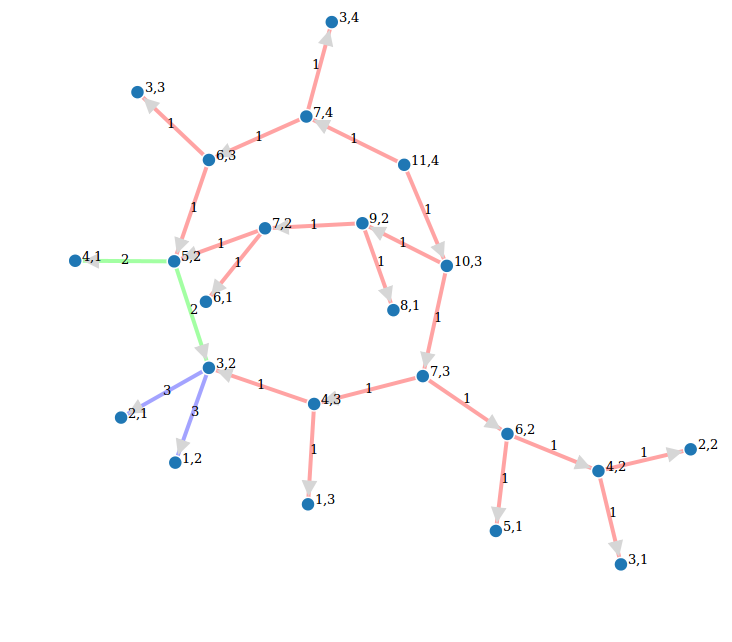

Very nice. Why do you ignore `**kwds`?
I need the set of args to be a short string, otherwise the graph is a mess. Plus, I didn't feel the need: do you have some example in mind?
No, not really. Just curious. The fact that you declared them in the method definition, but then never used them just left me wondering.
Your're right. BTW, I'm trying to add screenshots with no success... I had to upload the screenshots to the sagemath wiki...