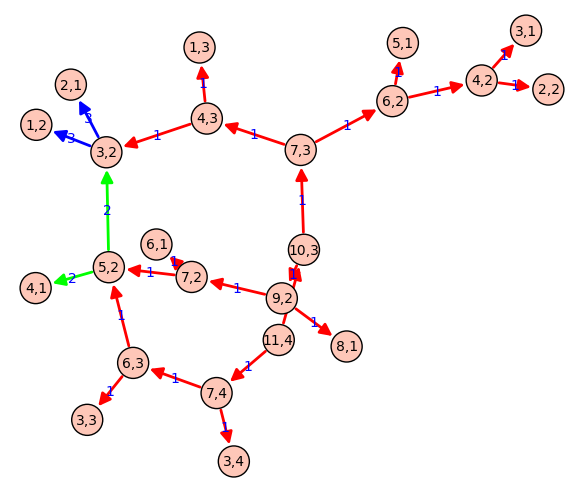
A colleague asked if I could write some code to show the call graph of a recursive function. I came up with this:
https://sage.mat.uam.es/pub/16/
def grafo_llamadas(f):
class G(object):
def __init__(self, f):
self.f=f
self.stack = []
self.g = DiGraph()
def __call__(self, *args, **kwds):
if self.stack:
sargs = ','.join(str(a) for a in args)
last = ','.join(str(a) for a in self.stack[-1])
if self.g.has_edge(last, sargs):
l = self.g.edge_label(last, sargs)
self.g.set_edge_label(last, sargs, l + 1)
else:
self.g.add_edge(last, sargs, 1)
else:
self.g = DiGraph()
self.stack.append(args)
v = self.f(*args)
self.stack.pop()
return v
def grafo(self):
return self.g
return G(f)
@grafo_llamadas
def fibo(n):
if n<=2:
return 1
else:
return fibo(n-1) + fibo(n-2)
fibo(6)
g = fibo.grafo()
g.show(edge_labels=True)
@grafo_llamadas
def particiones(n, k):
if k == n:
return [[1]*n]
if k == 1:
return [[n]]
if not(0 < k < n):
return []
ls1 = [p+[1] for p in particiones(n-1, k-1)]
ls2 = [[parte+1 for parte in p] for p in particiones(n-k, k)]
return ls1 + ls2
particiones(8,3)
g = particiones.grafo()
g.show(edge_labels=True, figsize=(8,8), vertex_size=500)
Do you like it? Can you improve it?