Revision history [back]
 | 1 | initial version |
It seems that the polynomial f itself does not contain the good information. Maybe 500 bits of precision is not enough?
sage: f.parent()
Multivariate Polynomial Ring in u, v over Real Field with 500 bits of precision
Because when I draw its roots with:
def plot_roots_of_f(start,stop,step):
u_range = srange(start, stop, step)
L = [(u,v) for u in u_range
for v in f.subs(u=u).univariate_polynomial().roots(multiplicities=False)
if (u,v) in P]
return points(L)
I get:
sage: G = plot_roots_of_f(1,20,.05) + plot_np
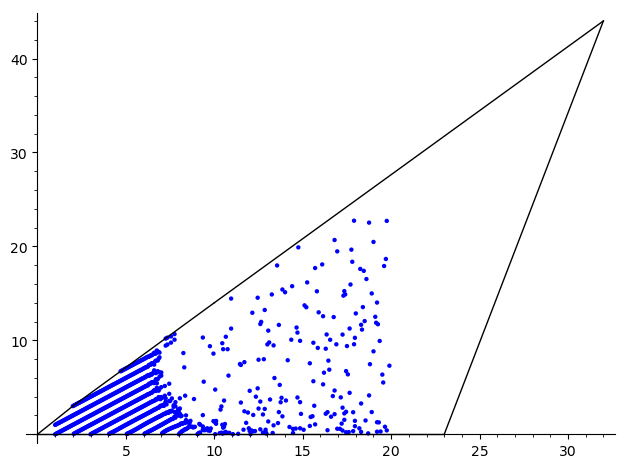
 | 2 | No.2 Revision |
It seems that the polynomial f itself does not contain the good information. Maybe 500 bits of precision is not enough?information.
sage: f.parent()
Multivariate Polynomial Ring in u, v over Real Field with 500 bits of precision
Because when I draw its roots with:
def plot_roots_of_f(start,stop,step):
u_range = srange(start, stop, step)
L = [(u,v) for u in u_range
for v in f.subs(u=u).univariate_polynomial().roots(multiplicities=False)
if (u,v) in P]
return points(L)
I get:
sage: G = plot_roots_of_f(1,20,.05) + plot_np

Replacing u and v by x and y to use the ring over the rational field seems to give the same thing.
sage: R
Multivariate Polynomial Ring in x, y over Rational Field
Are you sure about that polynomial f ?
 | 3 | No.3 Revision |
It seems that the polynomial f itself does not contain the good information.
sage: f.parent()
Multivariate Polynomial Ring in u, v over Real Field with 500 bits of precision
Because when I draw its roots with:
def plot_roots_of_f(start,stop,step):
u_range = srange(start, stop, step)
L = [(u,v) for u in u_range
for v in f.subs(u=u).univariate_polynomial().roots(multiplicities=False)
if (u,v) in P]
return points(L)
point(L) # I am using `point` here because the sage function `points` is a list in your code
I get:
sage: plot_roots_of_f(1,20,.05) + plot_np

Replacing u and v by x and y to use the ring over the rational field seems to give the same thing.
sage: R
Multivariate Polynomial Ring in x, y over Rational Field
Are you sure about that polynomial f ?
 | 4 | No.4 Revision |
It seems that the polynomial f itself does not contain the good information.
sage: f.parent()
Multivariate Polynomial Ring in u, v over Real Field with 500 bits of precision
Because when I draw its roots with:
def plot_roots_of_f(start,stop,step):
u_range = srange(start, stop, step)
L = [(u,v) for u in u_range
for v in f.subs(u=u).univariate_polynomial().roots(multiplicities=False)
if (u,v) in P]
return point(L) # I am using `point` here because the sage function `points` is a list in your the code
I get:
sage: plot_roots_of_f(1,20,.05) + plot_np

Replacing u and v by x and y to use the ring over the rational field seems to give the same thing.
sage: R
Multivariate Polynomial Ring in x, y over Rational Field
Are you sure about that polynomial f ?
 | 5 | No.5 Revision |
It seems that the polynomial f itself does not contain the good information.
sage: f.parent()
Multivariate Polynomial Ring in u, v over Real Field with 500 bits of precision
Because when I draw its roots with:
def plot_roots_of_f(start,stop,step):
u_range = srange(start, stop, step)
L = [(u,v) for u in u_range
for v in f.subs(u=u).univariate_polynomial().roots(multiplicities=False)
if (u,v) in P]
return point(L) # using `point` because the sage function `points` is a list in the code
I get:
sage: plot_roots_of_f(1,20,.05) + plot_np

Replacing u and v by x and y to use the ring over the rational field seems to give the same thing.
sage: R
Multivariate Polynomial Ring in x, y over Rational Field
Are you sure about that polynomial f ?
 | 6 | No.6 Revision |
It seems that the polynomial f itself does not contain the good information.
sage: f.parent()
Multivariate Polynomial Ring in u, v over Real Field with 500 bits of precision
Because when I draw its roots with:
def plot_roots_of_f(start,stop,step):
u_range = srange(start, stop, step)
L = [(u,v) for u in u_range
for v in f.subs(u=u).univariate_polynomial().roots(multiplicities=False)
if (u,v) in P]
return point(L) # using `point` because the sage function `points` is a list in the code
I get:
sage: plot_roots_of_f(1,20,.05) + plot_np

Replacing u and v by x and y to use the ring over the rational field seems to give the same thing.
sage: R
Multivariate Polynomial Ring in x, y over Rational Field
Are you sure about that polynomial f ?
sage: f.subs(u=20)
0
 | 7 | No.7 Revision |
It seems that the polynomial f itself does not contain the good information.
sage: f.parent()
Multivariate Polynomial Ring in u, v over Real Field with 500 bits of precision
Because when I draw its roots with:
def plot_roots_of_f(start,stop,step):
roots_of_f(start,stop,step):
u_range = srange(start, stop, step)
L = [(u,v) for u in u_range
for v in f.subs(u=u).univariate_polynomial().roots(multiplicities=False)
if (u,v) in P]
return point(L) # using `point` because the sage function `points` L
I get (points is a list in the code
code and overwrites the sage function points, so I get:
sage: plot_roots_of_f(1,20,.05) am using point below): sage: point(roots_of_f(1,20,.05))
+ plot_np

Replacing u and v by x and y to use the ring over the rational field seems to give the same thing.
sage: R
Multivariate Polynomial Ring in x, y over Rational Field
Are you sure about that polynomial f ? because the following seems weird:
sage: f.subs(u=20)
0
