Revision history [back]

I am attempting to solve and graph a system of differential equations. My setup is as follows:

I am able to successfully evaluate and graph if I set the variable 'mu' as a constant:

but otherwise Maxima says that it cannot understand my expression.

Where am I going wrong?

Thank you for your patience - I just started using SAGE this morning.

• Brandon

I am attempting to solve and graph the solution to an initial value problem containing a system of differential equations. My setup If I am remembering calculus correctly, its properties (nonlinear, ordinary, no explicit appearance of the independent variable time) classify it as a 'time-invariant autonomous system'.

I want to model a situation in which a microorganism in a bioreactor at some concentration 'X' is as follows:

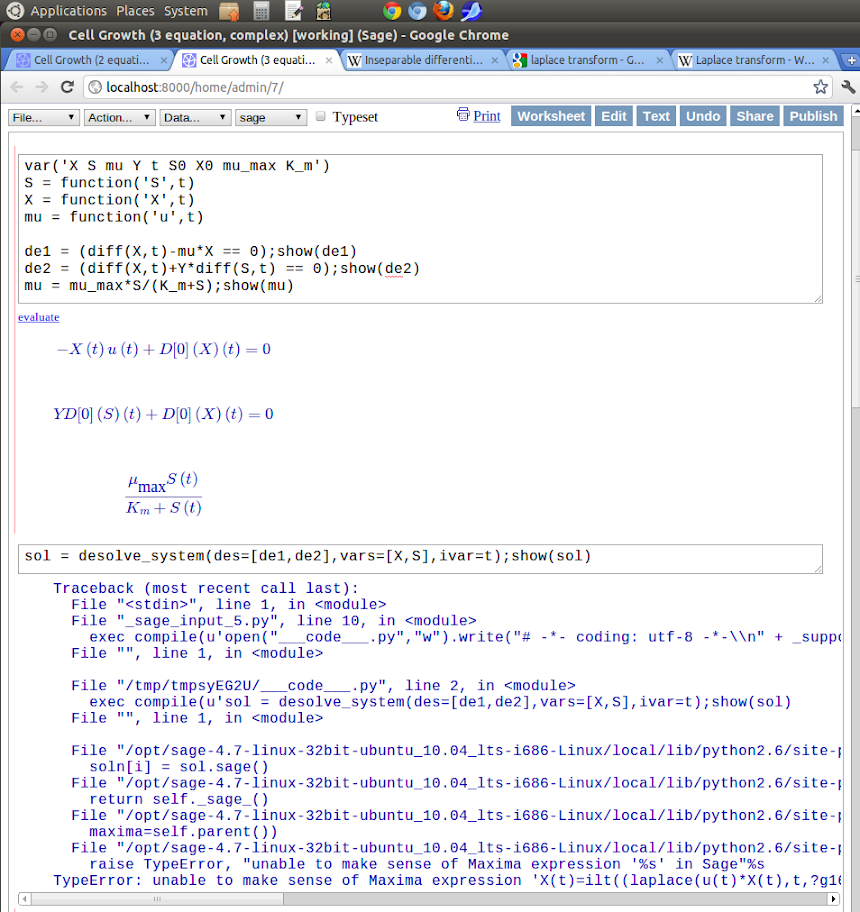
I am able to successfully growing exponentially 'dX/dt = u*X' by consuming a substrate at some concentration 'S'.

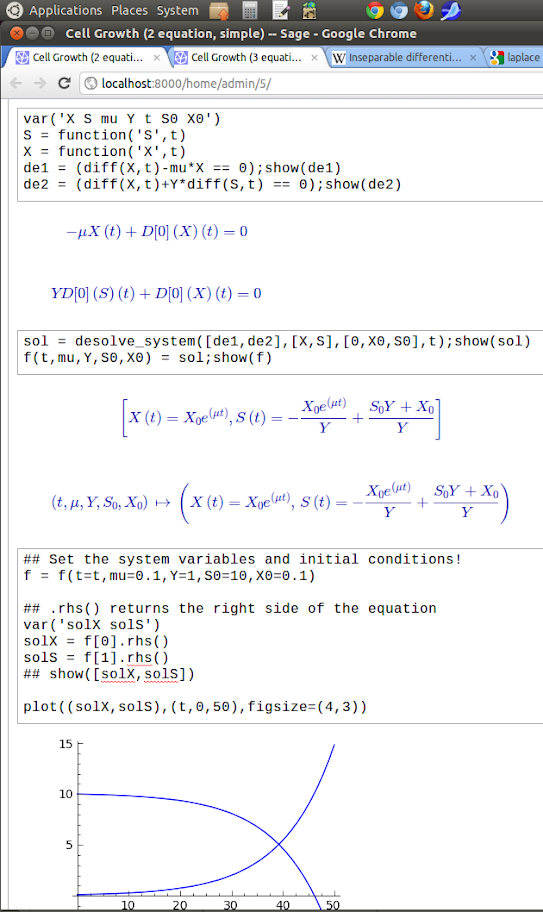
Substrate consumption '-dS/dt' and microorganism growth rate 'dX/dt' are related by a constant representing the yield of biomass on substrate, Y. If I stop here and leave the specific growth rate 'u' a constant, I can evaluate and graph if I set the variable 'mu' as a constant: this just fine with desolve_system():

but otherwise Maxima says The problems start when I make 'u' (specific growth rate) a function of 'S' (substrate concentration):
u = u_max*S/(K_m+S).

I make the assumption that it cannot understand my expression.this must be evaluated numerically, and switch to desolve_system_rk4(). I get an "Error executing code in Maxima", which also states "in definition f_rk_4, found bad argument 'X(t)"

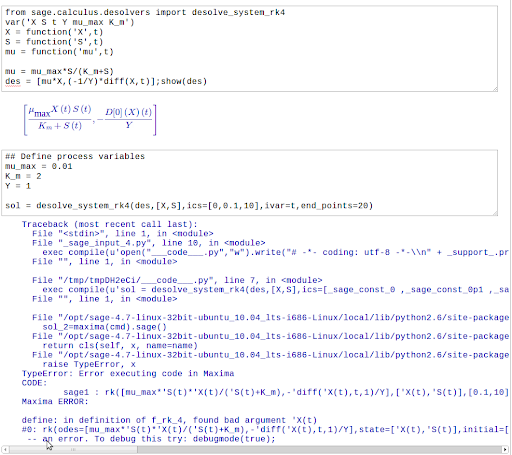
Where am I going wrong?wrong? Can I use desolve_system_rk4() to evaluate this system, and I'm just making a syntax error?

Thank you for your patience - I just started using SAGE this morning.yesterday.

• Brandon