This question is linked to the question https://ask.sagemath.org/question/68450/access-to-all-the-coefficients-of-an-expression-seems-to-fail/
Is there a bug in substitution of a function in SageMath? In asking the former question I have seen an error in the result but I was thinking it was my fact. After analysing the code and the result I have discovered an error in the substitution.
I rewrite only the necessary part of the code
def use_prime(expr):
"""
Return the expression with one-variable function derivatives "prime
"""
op = expr.operator()
if op:
args = expr.operands()
aargs = (use_prime(a) for a in args)
opp = op
if (isinstance(op, sage.symbolic.operators.FDerivativeOperator)and len(args) == 1):
name = op.function().name()
primes = "’" * len(op.parameter_set())
opp = function(f"{name}{primes}")
return opp(*aargs)
else:
return expr
##########################
var('x y p w_0 θ I')
assume(p>=0)
assume(p<=1)
assume(θ>=1)
U = function('U')#déclare U comme le nom d'une fonction
EU(x,y,p) = p * U(x) + (1-p) * U(y)
w_1 = function('w_1')
w_1(w_0, π) = (w_0-π)
w_2 = function('w_2')
w_2(w_0, π, x, I, p) = (w_0 - π) - x + I
π = function('π')
π(p,I,θ)=θ*(1-p)*I
U = function('U')
EU(x, y, p) = p*U(x) + (1 - p)*U(y)
x, y, p, w_0, θ, I, = SR.var('x y p w_0 θ I')
f = EU(w_1(w_0, π(p,I,θ)),w_2(w_0, π, x, I, π(p,I,θ)) )
h = diff(f, I)
hh = use_prime(h)
k = diff(f, I,2)
kk = use_prime(k)
show(LatexExpr(r'''\text{L'assuré cherche à résoudre le programme suivant :} '''))
show(LatexExpr(r'''I^\star= \textrm{argmax}_{\{I\}}\left\{pU(w_1)+(1-p) U(w_2)| w_1=w_0 - \pi, w_2=w_0 - \pi -x + I, \pi = \theta(1-p)I \right\} '''))
show(LatexExpr(r'''\text{ou encore : } I^\star = \textrm{argmax}_{\{I\}}\{'''), f,LatexExpr(r'\}'))
show(LatexExpr(r'''\text{La condition d'optimalité du premier ordre est } d\mathbb{E}U = 0 \text{, soit : } ''' ))
show(LatexExpr(r'\,\,\,\,\,\,\,\,\,\,\,\,\,\, d\mathbb{E}U = '),hh, ' = 0')
The result is
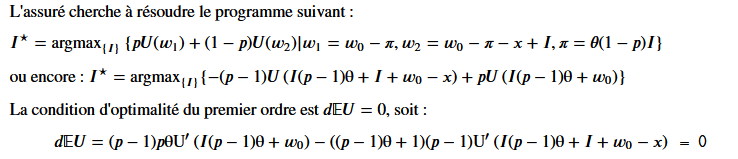
notice that $\pi = \theta (1-p)I$ which is rewriten directly by Sagemath $\pi = - \theta (p-1) I$ we must add the * of course. But if you look to the definition of $I^\star$ after the substitution the negative signe has disapeared inside $U()$.
Why ?

