I have encoutered a strange behavior in solving a linear program.
def sol_zero_sum_game(M=matrix([[1,-1], [-1,1]]),code=1) :
dim = M.nrows()
U=ones_matrix(dim,dim)
zsg=MixedIntegerLinearProgram(maximization=False, solver="GLPK")
x=zsg.new_variable(real=True,nonnegative=True, indices=[0..dim-1])
minM=min(min(M))
Id= identity_matrix(dim)
M1=(abs(minM)+1)*U+M
Bzsgl=M1*x
zsg.set_objective(sum(x[i] for i in range(dim)))
zsg.solve()
xx=zsg.get_values(x)
#show(xx)
for i in range(0,dim) :
zsg.add_constraint(Bzsgl[i]>=1)
if code==1 :
return zsg.show()
if code==2 :
return xx
The above code can display the program for the following G matrix :
G=matrix([[1,-1], [-1,1]])
sol_zero_sum_game(G,1)
The solution is given by :
G=matrix([[1,-1], [-1,1]])
sol_zero_sum_game(G,2)
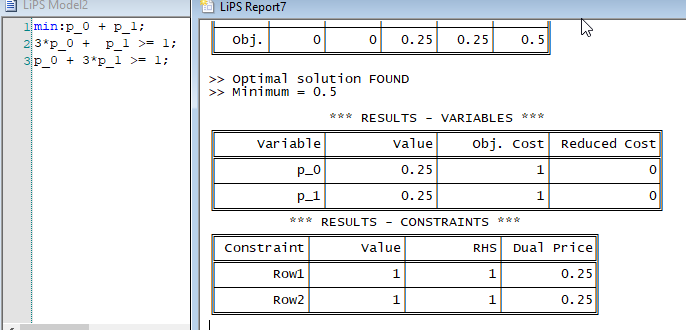
which gives {0: 0.0, 1: 0.0} as a solution. But this is obviously false since after substitution of $(0,0)$ in the constrains it doesn't work. As this is the formalisation of a game I know that the solution is $(0.25, 0.25)$ as confirmed by an other software LIPS (see the screen capture below).
I have certainly made a mistake but I can't see where. Thanks for help.


