plotting origin location
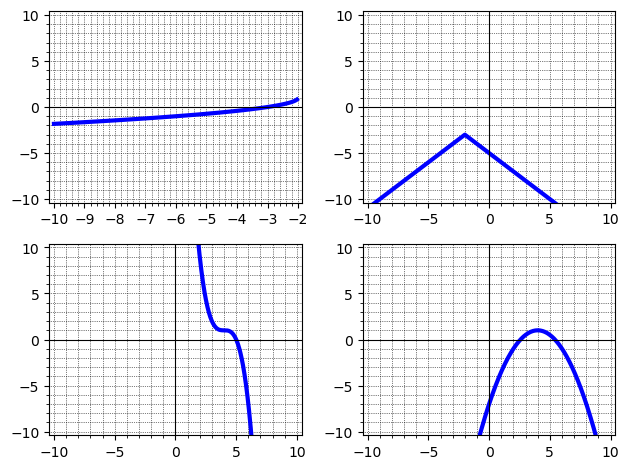
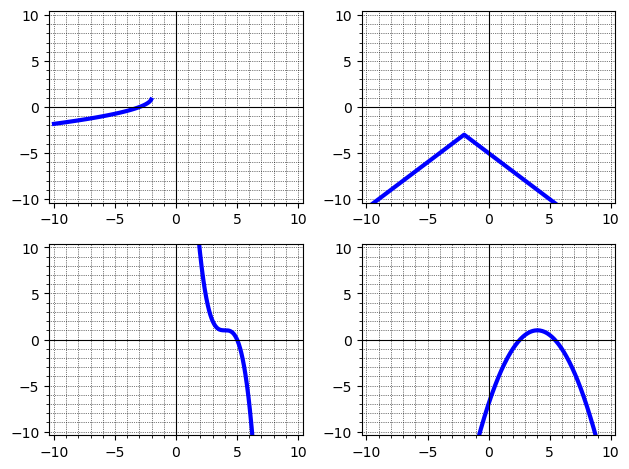
plotting some basic functions in sage, quadratic, abs value, etc. Then setting four up in an array. Problem; the square root function plots, but the frame and axes adjust so only the defined values show on the axes, and the origin and y axis are moved to the far left of the frame, not in the center, the image below will show the problem. Cannot find a way to remedy this, and plot the square root so the axes and frame stay put, i.e. centered, like the other three functions plot. Here is the code;
p1 = plot(-sqrt(-x-2)+1, (x,-10,8),xmin=-10,xmax=10,ymin=-10,ymax=10,gridlines="minor",frame=True,axes=True,figsize=(3,3),thickness='3') # the function ,followed by the domain
p2 = plot(-abs(x+2)-3, (x,-10,10),xmin=-10,xmax=10,ymin=-10,ymax=10,gridlines="minor",frame=True,figsize=(3,3),thickness='3')
p3= plot(-(x-4)^3+1, (x,-10,10),xmin=-10,xmax=10,ymin=-10,ymax=10,gridlines="minor",frame=True,figsize=(3,3),thickness='3') # the function ,followed by the domain
p4= plot(-.5*(x-4)^2+1, (x,-10,10),xmin=-10,xmax=10,ymin=-10,ymax=10,gridlines="minor",frame=True,figsize=(3,3),thickness='3') # the function ,followed by the domain
combined=myplot+myplot2
(myplot).show(title='A',frame=True,figsize=(5,5))
graphics_array(((p1,p2), (p3,p4))) # long time
Graphics Array of size 2 x 2
Here is the output; (Sorry, new user, cannot upload a file)