Some "strange behaviors“ of longest_path

edit

version: Sage 10.

I want to find a longest path starting from a given vertex in a graph. Below is my graph, and I have observed that if the longest path starting from a given vertex is a Hamiltonian path, longest_path responds very quickly. However, if it is not a Hamiltonian path, the response time is slow.

g1=Graph({0: [2, 3, 4, 15], 1: [16, 2, 3, 15], 2: [0, 1, 3, 4], 3: [0, 1, 2, 4], 4: [0, 2, 3, 15], 5: [7, 8, 9, 14], 6: [16, 7, 8, 9], 7: [5, 6, 8, 9], 8: [5, 6, 7, 9], 9: [5, 6, 7, 8], 10: [11, 12, 13, 14], 11: [16, 10, 12, 13], 12: [10, 11, 13, 14], 13: [16, 10, 11, 12], 14: [5, 10, 12, 15], 15: [0, 1, 4, 14], 16: [1, 6, 11, 13]})

Here is the calculation process.

 g1.longest_path(1) # quckily 
 g1.longest_path(14) # long time, about 100s

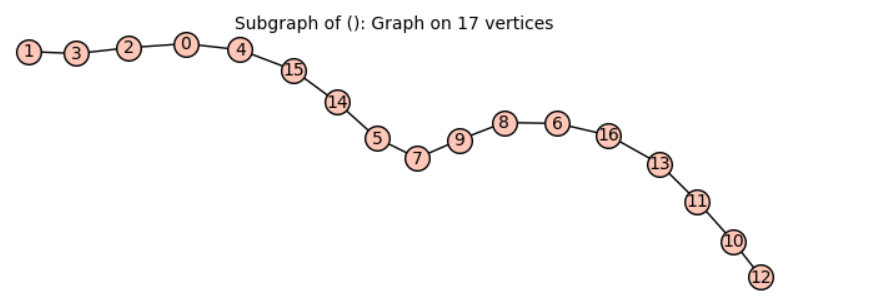
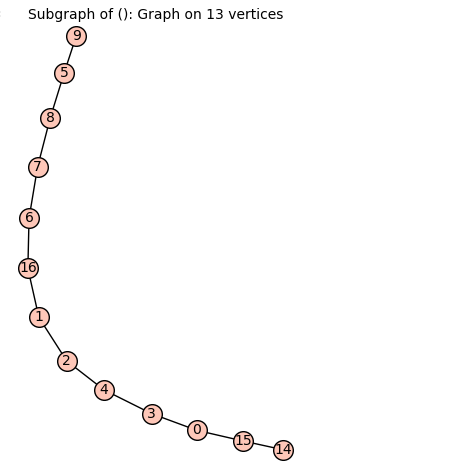
Additionally, I have noticed that the option backtracking in longest_pathdoes not seem to work when we specify the starting vertex. Looking at the output below, it is 1 or 9, not the longest path starting from vertex 14.

g1.longest_path(14,algorithm="backtrack")

Question 1. Why is there such a significant difference between the two cases?( When a vertex is given and there exists a Hamiltonian path that contains it as the starting vertex, it is puzzling why it is found quickly, while non-Hamiltonian paths take much longer.)

Question 2. Does the backtracking method not work when a starting vertex is given?