Naive approach:
sage: z, u = SR.var("z, u")
sage: Ex = 3*z^2 / (2 - 12*z^2 + sqrt(1 - 12*z^2)) - u
sage: %time Sol0 = solve(Ex, z)
CPU times: user 1.47 s, sys: 146 ms, total: 1.62 s
Wall time: 1.59 s
sage: Sol0
[z == -sqrt(1/3)*sqrt((sqrt(-12*z^2 + 1)*u + 2*u)/(4*u + 1)),
z == sqrt(1/3)*sqrt((sqrt(-12*z^2 + 1)*u + 2*u)/(4*u + 1))]
Your equation has a rational function with radicals of a polynomial in your variable of interest. Sage's default solver is unable to solve it, and returns a (set of) equation(s) equivalent to the original one (an implicit solution) :
Let's try a variant of Maxima's solver (see solve? for details):
sage: %time Sol1 = solve(Ex, z, to_poly_solve=True)
CPU times: user 2min 15s, sys: 959 ms, total: 2min 16s
Wall time: 1min 35s
sage: Sol1
[z == -sqrt(1/3)*sqrt((sqrt(-12*z^2 + 1)*u + 2*u)/(4*u + 1)),
z == sqrt(1/3)*sqrt((sqrt(-12*z^2 + 1)*u + 2*u)/(4*u + 1))]
Takes its sweet time, and returns the same (non-)solution.
Force the use of the alternate algorithm :
sage: %time Sol2 = solve(Ex, z, to_poly_solve="force")
CPU times: user 30.9 s, sys: 243 ms, total: 31.1 s
Wall time: 21.8 s
sage: Sol2
[]
SOL...
Let's get rid of the radicals, by squaring the equations until there is no radical. It can be done manually, or you can a Sympy utility for this:
sage: from sympy.solvers.solvers import unrad
sage: foo = unrad(Ex._sympy_())
sage: foo
(48*u**2*z**4 - 12*u**2*z**2 + u**2 + 24*u*z**4 - 4*u*z**2 + 3*z**4, [])
foo[0] is a (Sympy) polynomial in u and z whose roots are a superset of those of Ex (see unrad? for details).
We can try to solve it for z to get a set of candidate solutions (by squaring, we may have introduced spurious solutions...) :
sage: %time CSol = solve(foo[0]._sage_(), z); CSol
CPU times: user 15.2 ms, sys: 0 ns, total: 15.2 ms
Wall time: 15.2 ms
[z == -sqrt(2*u^2 + 1/3*sqrt(-12*u^2 + 1)*u + 2/3*u)/(4*u + 1),
z == sqrt(2*u^2 + 1/3*sqrt(-12*u^2 + 1)*u + 2/3*u)/(4*u + 1),
z == -sqrt(2*u^2 - 1/3*sqrt(-12*u^2 + 1)*u + 2/3*u)/(4*u + 1),
z == sqrt(2*u^2 - 1/3*sqrt(-12*u^2 + 1)*u + 2/3*u)/(4*u + 1)]
However, filtering the "real" solutions isn't easy: Sage is currently unable to check those candidate solutions:
sage: [Ex.subs(s).is_zero() for s in CSol]
[False, False, False, False]
This filtering may be possible by numerical checks in a "likely" region of u values. Rapid checks for u in the [-5, 5] real interval found no valid solution.
Using Sympy directly returns a set of possible implicit solutions:
sage: solve(Ex, z, algorithm="sympy")
Complement(ConditionSet(z, Eq(u/3 + z**2/(12*z**2 - sqrt(1 - 12*z**2) - 2), 0), {-sqrt(6*u**2/(48*u**2 + 24*u + 3) - u*sqrt(1 - 12*u**2)/(48*u**2 + 24*u + 3) + 2*u/(48*u**2 + 24*u + 3)), sqrt(6*u**2/(48*u**2 + 24*u + 3) - u*sqrt(1 - 12*u**2)/(48*u**2 + 24*u + 3) + 2*u/(48*u**2 + 24*u + 3)), -sqrt(6*u**2/(48*u**2 + 24*u + 3) + u*sqrt(1 - 12*u**2)/(48*u**2 + 24*u + 3) + 2*u/(48*u**2 + 24*u + 3)), sqrt(6*u**2/(48*u**2 + 24*u + 3) + u*sqrt(1 - 12*u**2)/(48*u**2 + 24*u + 3) + 2*u/(48*u**2 + 24*u + 3))}), ConditionSet(z, Eq(12*z**2 - sqrt(1 - 12*z**2) - 2, 0), {-sqrt(2)*3**(1/4)/8 - sqrt(2)*3**(3/4)/24 + I*(-sqrt(2)*3**(1/4)/8 + sqrt(2)*3**(3/4)/24), -sqrt(2)*3**(1/4)/8 - sqrt(2)*3**(3/4)/24 + I*(-sqrt(2)*3**(3/4)/24 + sqrt(2)*3**(1/4)/8), sqrt(2)*3**(3/4)/24 + sqrt(2)*3**(1/4)/8 + I*(-sqrt(2)*3**(1/4)/8 + sqrt(2)*3**(3/4)/24), sqrt(2)*3**(3/4)/24 + sqrt(2)*3**(1/4)/8 + I*(-sqrt(2)*3**(3/4)/24 + sqrt(2)*3**(1/4)/8)}))
which is no more checkable than the previous ones...
Querying "the competition" (Mathematica) via WolframAlpha may be instructive.
My first attempts do not make me optimist...
EDIT: A bit of numerical check leads me to think
that the first two solutions are valid in a small region
of the Argand plane around 0:
sage: f = lambda t, v: Ex.subs(CSol[2*t + v]).function(u)
sage: cplot = lambda t, v: complex_plot(f(t, v), (-1, 1), (-1, 1), plot_points=200)
sage: graphics_array([[cplot(t, v) for v in range(2)] for t in range(2)])
Launched png viewer for Graphics Array of size 2 x 2
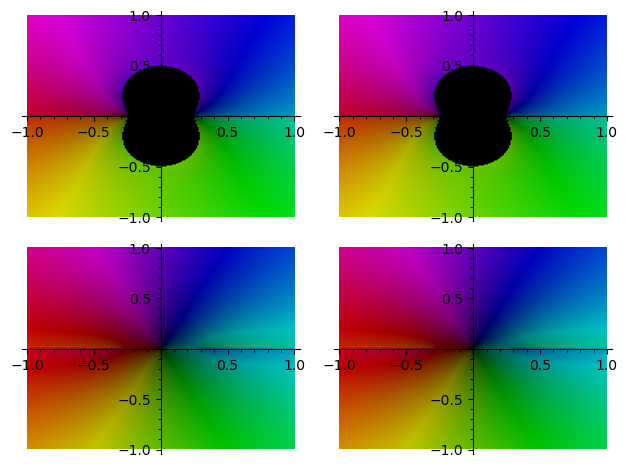
I have (currently) no idea of the reason of this region of validity. Someone with better knowledge of the behaviour of the (complex) rational functions is welcome to explain it...
EDIT 2 : "The competition" gives a formally different answer, which seems to lead to numerically similar validity regions of the roots.
Please disregard a previous version of this edit, which claimed to have found a failure...
sage: foo=mathematica("Sol=Solve[%s, %s]"%tuple(map(lambda u:repr(mathematica(u)), (Ex==0, z))))
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
Cell In [3], line 1
----> 1 foo=mathematica("Sol=Solve[%s, %s]"%tuple(map(lambda u:repr(mathematica(u)), (Ex==Integer(0), z))))
File /usr/local/sage-10/src/sage/misc/lazy_import.pyx:404, in sage.misc.lazy_import.LazyImport.__call__()
402 True
403 """
--> 404 return self.get_object()(*args, **kwds)
405
406 def __repr__(self):
File /usr/local/sage-10/src/sage/interfaces/interface.py:298, in Interface.__call__(self, x, name)
295 pass
297 if isinstance(x, str):
--> 298 return cls(self, x, name=name)
299 try:
300 # Special methods do not and should not have an option to
301 # set the name directly, as the identifier assigned by the
302 # interface should stay consistent. An identifier with a
303 # user-assigned name might change its value, so we return a
304 # new element.
305 result = self._coerce_from_special_method(x)
File /usr/local/sage-10/src/sage/interfaces/expect.py:1496, in ExpectElement.__init__(self, parent, value, is_name, name)
1494 else:
1495 try:
-> 1496 self._name = parent._create(value, name=name)
1497 # Convert ValueError and RuntimeError to TypeError for
1498 # coercion to work properly.
1499 except (RuntimeError, ValueError) as x:
File /usr/local/sage-10/src/sage/interfaces/interface.py:516, in Interface._create(self, value, name)
514 def _create(self, value, name=None):
515 name = self._next_var_name() if name is None else name
--> 516 self.set(name, value)
517 return name
File /usr/local/sage-10/src/sage/interfaces/mathematica.py:621, in Mathematica.set(self, var, value)
619 out = self._eval_line(cmd, allow_use_file=True)
620 if len(out) > 8:
--> 621 raise TypeError("Error executing code in Mathematica\nCODE:\n\t%s\nMathematica ERROR:\n\t%s" % (cmd, out))
TypeError: Error executing code in Mathematica
CODE:
sage0=Sol=Solve[-u - (3*z^2)/(-2 + 12*z^2 - Sqrt[1 - 12*z^2]) == 0, z];
Mathematica ERROR:
Solve::nongen: There may be values of the parameters for which some or all
solutions are not valid.
Here, Sage wrongly interprets a Mathematica warning as an error, hence the workaround... The solutions can be (manually) transtlated in Sage :
sage: MSol=[{u[1].sage():u[2].sage() for u in s} for s in mathematica("Sol")] ; MSol
[{z: -1/3*sqrt(3)*sqrt(6*u^2/(16*u^2 + 8*u + 1) + 2*u/(16*u^2 + 8*u + 1) - sqrt(-(12*u^2 - 1)*u^2)/(16*u^2 + 8*u + 1))},
{z: 1/3*sqrt(3)*sqrt(6*u^2/(16*u^2 + 8*u + 1) + 2*u/(16*u^2 + 8*u + 1) - sqrt(-(12*u^2 - 1)*u^2)/(16*u^2 + 8*u + 1))},
{z: -sqrt(2*u^2/(16*u^2 + 8*u + 1) + 2/3*u/(16*u^2 + 8*u + 1) + 1/3*sqrt(-12*u^4 + u^2)/(16*u^2 + 8*u + 1))},
{z: sqrt(2*u^2/(16*u^2 + 8*u + 1) + 2/3*u/(16*u^2 + 8*u + 1) + 1/3*sqrt(-12*u^4 + u^2)/(16*u^2 + 8*u + 1))}]
and (numerically) checked :
sage: graphics_array([[complex_plot(Ex.subs(MSol[2*u+v]), (-1, 1), (-1, 1), plot_points=200) for v in range(2)] for u in range(2)])
Launched png viewer for Graphics Array of size 2 x 2
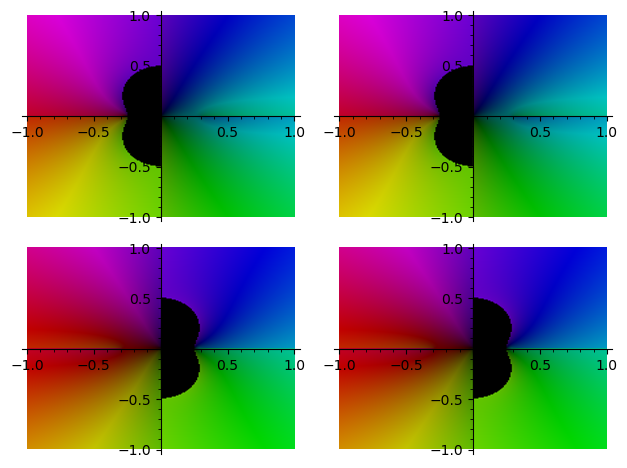
Sorry not to be more helpful.


