Minus sign lost in substitution

edit

This question is related to a previous question:

• Ask Sage question 68450: Access to all the coefficients of an expression seems to fail

Is there a bug in substitution of a function in SageMath?

In asking the former question I saw an error in the result but I thought it might be my fault.

After analysing the code and the result I have discovered an error in the substitution.

I rewrite only the necessary part of the code:

def use_prime(expr):
    """
    Return the expression with one-variable function derivatives in prime notation.
    """
    op = expr.operator()
    if op:
        args = expr.operands()
        aargs = (use_prime(a) for a in args)
        opp = op
        if (isinstance(op, sage.symbolic.operators.FDerivativeOperator)
                and len(args) == 1):
            name = op.function().name()
            primes = "’" * len(op.parameter_set())
            opp = function(f"{name}{primes}")
        return opp(*aargs)
    else:
        return expr

var('x y p w_0 θ I')
assume(p >= 0)
assume(p <= 1)
assume(θ >= 1)
U = function('U')  # déclare U comme le nom d'une fonction
EU(x, y, p) = p * U(x) + (1-p) * U(y)
w_1 = function('w_1')
w_1(w_0, π) = (w_0 - π)
w_2 = function('w_2')
w_2(w_0, π, x, I, p) = (w_0 - π) - x + I 
π = function('π')
π(p, I, θ) = θ * (1 - p) * I
U = function('U')
EU(x, y, p) = p * U(x) + (1 - p) * U(y)
x, y, p, w_0, θ, I, = SR.var('x y p w_0 θ I')
f = EU(w_1(w_0, π(p, I, θ)), w_2(w_0, π, x, I, π(p, I, θ)))
h = diff(f, I)
hh = use_prime(h)
k = diff(f, I, 2)
kk = use_prime(k)
show(LatexExpr(r'''\text{L’assuré cherche à résoudre le programme suivant :} '''))
show(LatexExpr(r'''I^\star = \textrm{argmax}_{\{I\}}\left\{pU(w_1)+(1-p) U(w_2)| w_1'''
               r''' = w_0 - \pi, w_2=w_0 - \pi -x + I, \pi = \theta(1-p)I \right\} '''))
show(LatexExpr(r'''\text{ou encore : } I^\star = \textrm{argmax}_{\{I\}}\{'''),
     f, LatexExpr(r'\}'))     
show(LatexExpr(r'''\text{La condition d’optimalité du premier ordre est } '''
               r'''d\mathbb{E}U = 0 \text{, soit : }'''))
show(LatexExpr(r'\,\,\,\,\,\,\,\,\,\,\,\,\,\, d\mathbb{E}U = '), hh, ' = 0')

The result is

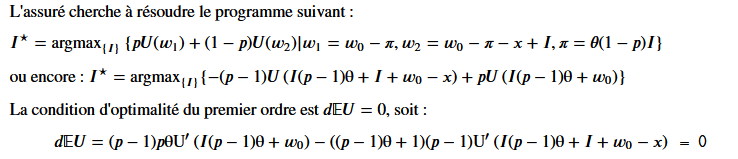
Notice that $\pi = \theta (1-p)I$ which is rewritten directly by SageMath as $\pi = - \theta (p-1) I$ we must add the * of course. But if you look at the definition of $I^\star$ after the substitution, the negative sign has disappeared inside $U()$.

Why?