This has to do with rewriting systems for groups given by presentations.
When a group G is defined as a quotient of the free group by some relations,
as in the question, elements in G are stored as words in the generators.
Deciding whether elements given by different words are equal in the group
is undecidable in general, although of course for some groups it is decidable.
Technically speaking, a rewriting system is associated with the group presentation.
A rewriting system is called confluent if it provides
a canonical representative for each group element.
The rewriting system associated with the group G
as defined in the question is not confluent.
sage: F.<x> = FreeGroup('x')
sage: G = F / [x^3]
sage: r = G.rewriting_system()
sage: r
Rewriting system of Finitely presented group < x | x^3 >
with rules:
x^3 ---> 1
sage: s = G.rewriting_system()
sage: s.make_confluent()
sage: s
Rewriting system of Finitely presented group < x | x^3 >
with rules:
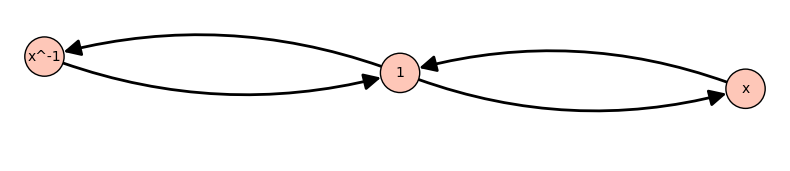
x^-2 ---> x
x^2 ---> x^-1
To compare the initial rewriting system and the confluent one:
sage: r.is_confluent()
False
sage: s.is_confluent()
True
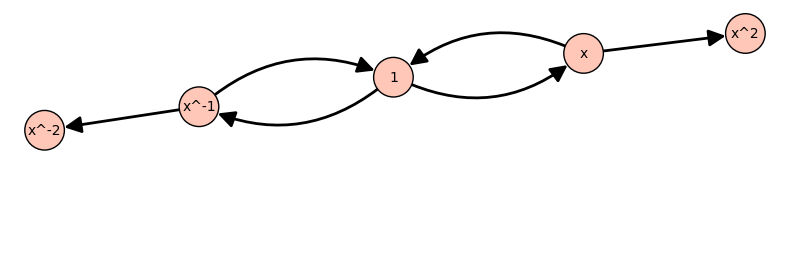
The initial one can only simplify positive multiples of 3 in the exponent,
while the confluent one gives a unique form with exponents between -1 and 1.
sage: a = " n x^n G(x^n) r(x^n) s(x^n)"
sage: b = "-------------------------------------"
sage: c = [(n, x^n, G(x^n), r.reduce(x^n), s.reduce(x^n)) for n in range(-5, 8)]
sage: print('\n'.join(['', a, b] + ["%3s %6s %8s %8s %8s" % t for t in c]))
n x^n G(x^n) r(x^n) s(x^n)
-------------------------------------
-5 x^-5 x^-5 x^-5 x
-4 x^-4 x^-4 x^-4 x^-1
-3 x^-3 x^-3 x^-3 1
-2 x^-2 x^-2 x^-2 x
-1 x^-1 x^-1 x^-1 x^-1
0 1 1 1 1
1 x x x x
2 x^2 x^2 x^2 x^-1
3 x^3 x^3 1 1
4 x^4 x^4 x x
5 x^5 x^5 x^2 x^-1
6 x^6 x^6 1 1
7 x^7 x^7 x x
For some groups, attempting to make the rewriting system confluent
will not terminate. This is why it is not done systematically.
The function my_cayley_graph below has an option to try and make
the rewriting system confluent.
When this succeeds, this guarantees a correct Cayley graph.
def my_cayley_graph(self, side="right", simple=False, elements=None,
generators=None, connecting_set=None,
make_rewriting_system_confluent=False):
r"""
Return the Cayley graph for this finite semigroup.
INPUT:
- ``side`` -- "left", "right", or "twosided":
the side on which the generators act (default:"right")
- ``simple`` -- boolean (default:False):
if True, returns a simple graph (no loops, no labels,
no multiple edges)
- ``generators`` -- a list, tuple, or family of elements
of ``self`` (default: ``self.semigroup_generators()``)
- ``connecting_set`` -- alias for ``generators``; deprecated
- ``elements`` -- a list (or iterable) of elements of ``self``
- ``make_rewriting_system_confluent`` -- whether to attempt
to make ``self``'s rewriting system confluent to compute
the Cayley graph (warning: this might not terminate)
Adapted from the `cayley_graph` method of semigroups, see Sage source code at
https://github.com/sagemath/sage/blob/9.8/src/sage/categories/semigroups.py#L174
OUTPUT:
- :class:`DiGraph`
EXAMPLES:
We illustrate the ``make_rewriting_system_confluent`` option::
sage: F.<x> = FreeGroup('x')
sage: G = F / [x^3]
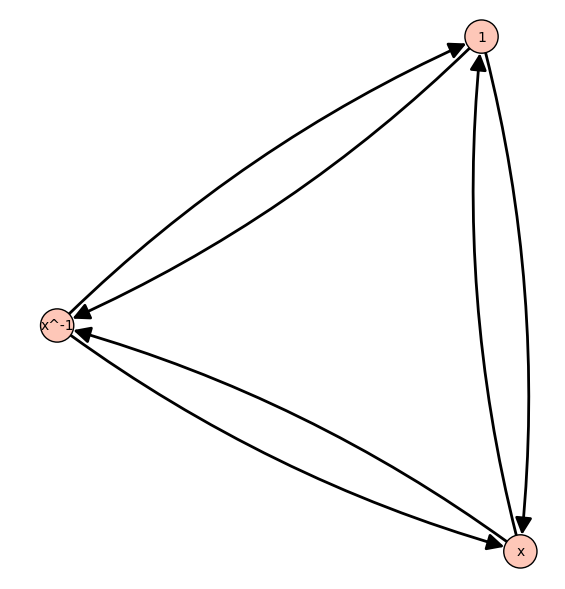
sage: C = my_cayley_graph(G, make_rewriting_system_confluent=True)
sage: C.vertices(sort=False), C.edges(sort=False)
([1, x, x^-1],
[(1, x, 0), (1, x^-1, 1), (x, 1, 1), (x, x^-1, 0), (x^-1, 1, 0), (x^-1, x, 1)])
AUTHORS:
- Bobby Moretti (2007-08-10)
- Robert Miller (2008-05-01): editing
- Nicolas M. Thiery (2008-12): extension to semigroups,
``side``, ``simple``, and ``elements`` options, ...
- Samuel Lelièvre (2023-05-19): add option to make rewriting system confluent
"""
from sage.graphs.digraph import DiGraph
from sage.categories.monoids import Monoids
from sage.categories.groups import Groups
if side not in ["left", "right", "twosided"]:
raise ValueError("option 'side' must be 'left', 'right' or 'twosided'")
if elements is None:
assert self.is_finite(), "elements should be specified for infinite semigroups"
elements = self
else:
elements = set(elements)
if simple or self in Groups():
result = DiGraph()
else:
result = DiGraph(multiedges=True, loops=True)
result.add_vertices(elements)
if connecting_set is not None:
generators = connecting_set
if generators is None:
if self in Monoids and hasattr(self, "monoid_generators"):
generators = self.monoid_generators()
else:
generators = self.semigroup_generators()
if isinstance(generators, (list, tuple)):
generators = dict((self(g), self(g)) for g in generators)
left = (side == "left" or side == "twosided")
right = (side == "right" or side == "twosided")
k = self.rewriting_system()
if make_rewriting_system_confluent:
k.make_confluent()
def add_edge(source, target, label, side_label):
r"""
Add an appropriate edge to ``result`` given the options.
Skips edges whose targets are not in ``elements``.
"""
source = k.reduce(source)
target = k.reduce(target)
if (elements is not self and target not in elements):
return
if simple:
if source != target:
result.add_edge([source, target])
elif side == "twosided":
result.add_edge([source, target, (label, side_label)])
else:
result.add_edge([source, target, label])
for x in elements:
for i in generators.keys():
if left:
add_edge(x, generators[i] * x, i, "left" )
if right:
add_edge(x, x * generators[i], i, "right")
return result
Example.
sage: F.<x> = FreeGroup('x')
sage: G = F / [x^3]
sage: C = my_cayley_graph(G, make_rewriting_system_confluent=True)
sage: C.vertices(sort=False), C.edges(sort=False)
([1, x, x^-1],
[(1, x, 0), (1, x^-1, 1), (x, 1, 1), (x, x^-1, 0), (x^-1, 1, 0), (x^-1, x, 1)])
sage: C
Digraph on 3 vertices
sage: C.plot()
Launched png viewer for Graphics object consisting of 12 graphics primitives