Find all minimal edge cuts of a graph.
An edge cut is a set of edges that, if removed from a connected graph, will disconnect the graph.
A minimal edge cut is an edge cut such that if any edge is put back in the graph, the graph will be reconnected.
A minimum edge cut is an edge cut such that there is no other edge cut containing fewer edges.
Note that a minimum edge cut is always minimal, but a minimal edge cut is not always minimum.
g="S~tIID@OI?{@n~V?goYEDOWd?qI?sJ?[C"
G = Graph(g, sparse=True);
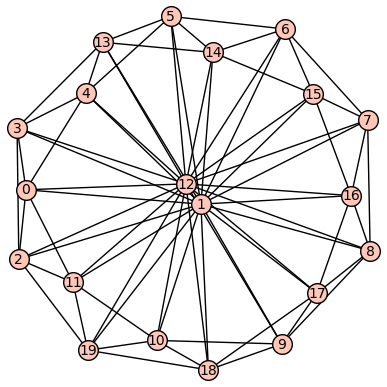
How to find its all minimal edge cuts? I have searched Literature [1] for the corresponding polynomial algorithm (which you can view). But I don't see any code implementation. For the above graph (with 20 vertices), perhaps a violent search would be possible.
[1] Karzanov, A.V., Timofeev, E.A. Efficient algorithm for finding all minimal edge cuts of a nonoriented graph. Cybern Syst Anal 22, 156–162 (1986). https://doi.org/10.1007/BF01074775

You can certainly implement the algorithm described in the paper.
@ David Coudert From the discussion below, it appears that there is no polynomial algorithm for finding all minimal cuts. I feel that I have misread Literature [1], or the result of Literature [1] itself is wrong.
(I don't know how I became an anonymous in this question)