How to get result - diophantines equation

edit

These exponential equation systems have no general solution, and no CAS accessible by Sage (i. e. Maxima, Giac, Fricas, Sympy nor the gratis Wolfram Engine) can "solve" it.

One may note that :

sage: f(x, y) = 16^(x^2 + y) + 16^(y^2 + x)
sage: implicit_plot(f-1, (-1, 1), (-1, 1))
/usr/local/sage-9/src/sage/plot/contour_plot.py:988: UserWarning: pathological contour plot of a function whose values all lie on one side of the sole contour; we are adding more plot points and perturbing your function values.
  warn("pathological contour plot of a function whose "
Launched png viewer for Graphics object consisting of 1 graphics primitive

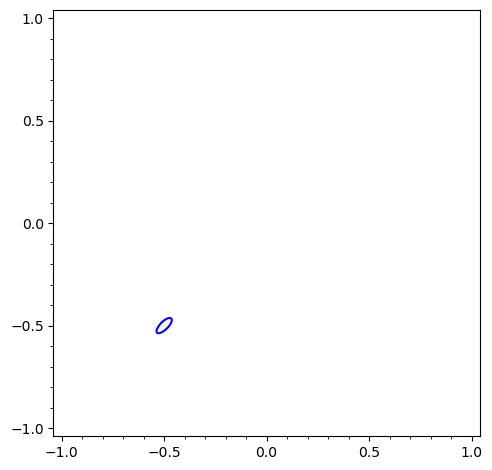
hints at a possible solution around (-0.5, -0.5). A bit of further numerical exploration (and a suitably large amount of bad faith) may lead to check :

sage: f(-1/2, -1/2)
1

proclaim it "an obvious root" and, while we are at it, check that it is a local minimum :

sage: f.diff()(-1/2, -1/2)
(0, 0)

Similarly, plot3d(f, (-5, 5), (-5, 5)).show(viewer="jmol") shows us a surface whose smallest z value is 1 on the considered domain.

The problem is now to show that this root is the only one possible, possibly by showing that this minimum is unique. A way would be to show that the surface representing is is always upwards-concave, i. e. that both the eigenvalues of its hessian are positive. This leads to study the inequation system :

sage: ISys = [u.canonicalize_radical()>0 for u in f.hessian()(x,y).eigenvalues()] ; ISys
[4*(8*x^2*log(2)^2 + 2*log(2)^2 + log(2))*2^(4*x^2 + 4*y) + (2^(4*x + 5)*y^2*log(2)^2 + 4*(2*log(2)^2 + log(2))*2^(4*x))*2^(4*y^2) - 4*sqrt((64*x^4*log(2)^2 + 16*(2*log(2)^2 + log(2))*x^2 + 4*log(2)^2 - 4*log(2) + 1)*2^(8*x^2 + 8*y) + (2^(8*x + 6)*y^4*log(2)^2 + 16*(2*log(2)^2 + log(2))*2^(8*x)*y^2 + (4*log(2)^2 - 4*log(2) + 1)*2^(8*x))*2^(8*y^2) + (2^(4*x^2 + 4*x + 7)*x*y*log(2)^2 - 16*(8*x^2*log(2)^2 - 2*log(2)^2 + log(2))*2^(4*x^2 + 4*x)*y^2 + 2*(8*(2*log(2)^2 - log(2))*x^2 - 4*log(2)^2 + 4*log(2) - 1)*2^(4*x^2 + 4*x))*2^(4*y^2 + 4*y))*log(2) > 0,
 4*(8*x^2*log(2)^2 + 2*log(2)^2 + log(2))*2^(4*x^2 + 4*y) + (2^(4*x + 5)*y^2*log(2)^2 + 4*(2*log(2)^2 + log(2))*2^(4*x))*2^(4*y^2) + 4*sqrt((64*x^4*log(2)^2 + 16*(2*log(2)^2 + log(2))*x^2 + 4*log(2)^2 - 4*log(2) + 1)*2^(8*x^2 + 8*y) + (2^(8*x + 6)*y^4*log(2)^2 + 16*(2*log(2)^2 + log(2))*2^(8*x)*y^2 + (4*log(2)^2 - 4*log(2) + 1)*2^(8*x))*2^(8*y^2) + (2^(4*x^2 + 4*x + 7)*x*y*log(2)^2 - 16*(8*x^2*log(2)^2 - 2*log(2)^2 + log(2))*2^(4*x^2 + 4*x)*y^2 + 2*(8*(2*log(2)^2 - log(2))*x^2 - 4*log(2)^2 + 4*log(2) - 1)*2^(4*x^2 + 4*x))*2^(4*y^2 + 4*y))*log(2) > 0]

which, again, none of the CASes accessible via Sage can show "easily".

One possible wau of attack is to note that both inequations' left-hand sides are sums ; finding suitable minorants of their terms and showing that they are positive would be enough to demonstrate the upward concavity and, therefore, the unicity of the minimum (and the root).

I'm too lazy for this. Maybe someone with more courage (or better ideas) might get this proof...

Another way could be to change coordinates to work in polar coordinates centered on -1/2, -1/2) and to show that $\displaystyle\frac{\partial^2 f}{\partial r^2}$ is positive. Again, I didn't pursue in this direction...

HTH,