i exponents of non integers

asked 2022-05-09 08:38:14 +0100

I'm not very good at math, but always had a creative interest. Especially when it came to imaginary numbers. The question that occurred to me is How do you graph Y=i multiplied by itself to the power of a non-whole number (I think the word is "non-integer?")? Would that be an indefinite "tube," for lack of better verbage, between -1 and 1? Tangenting off the "tube" remark, would it affect the Z or other different axis? I didn't make it past precalculus, and I'm not in school. Just a random curiosity, and I'm not sure if it has any real application. Thank you in advance for any time and attention you spend replying.

Comments

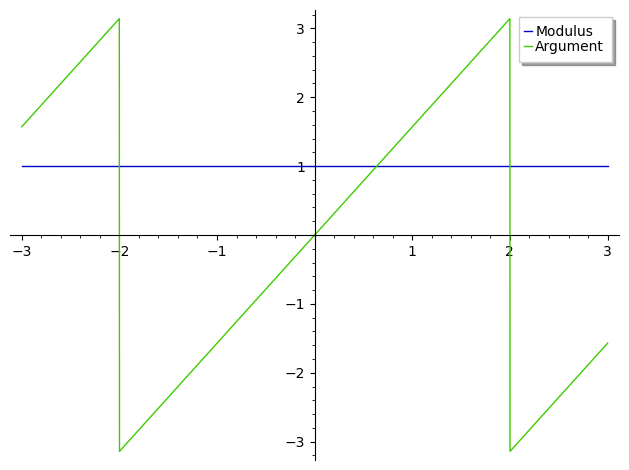
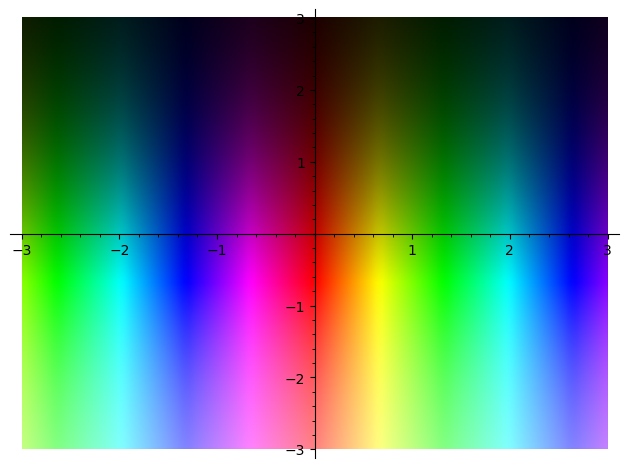
Trying :

plot([(I^x).abs(), (I^x).maxima_methods().arg()], (x, -3, 3), legend_label=["Modulus", "Argument"])

may enlighten you.

Emmanuel Charpentier ( 2022-05-09 15:16:10 +0100 )edit

add a comment

answered 2022-05-09 16:00:15 +0100

Emmanuel Charpentier
7774 ●6 ●51 ●154

updated 2022-05-09 16:05:23 +0100

As suggested above, a graphical representation gives an easy intuition :

plot([(I^x).abs(), (I^x).maxima_methods().arg()], (x, -3, 3), legend_label=["Modulus", "Argument"])

$Argument an modulus of $e^{ix}$$

To understand the result, try :

sage: var("a, b")
(a, b)
sage: E0=log(a^b)==log(a^b).log_expand() ; E0
log(a^b) == b*log(a)
sage: E1 =E0.subs([a==I, b==x]) ; E1
log(I^x) == 1/2*I*pi*x
sage: E2 = E1.operator()(*map(exp, E1.operands())) ; E2
I^x == e^(1/2*I*pi*x)

The latter may be easier to grasp in a different form :

sage: E2.rhs().demoivre(force=True)
cos(1/2*pi*x) + I*sin(1/2*pi*x)

Exercise for the (advanced) reader : try and understand :

complex_plot(I^x, (-3, 3), (-3, 3))

$Complex plot of $e^{iz}$$

Hint : look up the definitions of exp and trig functions for complexes...

HTH,

edit flag offensive delete link

add a comment

Your Answer

Please start posting anonymously - your entry will be published after you log in or create a new account.

i exponents of non integers

Comments

1 Answer

Your Answer

Question Tools

Stats

Related questions

i exponents of non integers edit

Comments

1 Answer

Your Answer

Question Tools

Stats

Related questions

i exponents of non integers