Revision history [back]
 | 1 | initial version |
As suggested above, a graphical representation gives an easy intuition :
plot([(I^x).abs(), (I^x).maxima_methods().arg()], (x, -3, 3), legend_label=["Modulus", "Argument"])
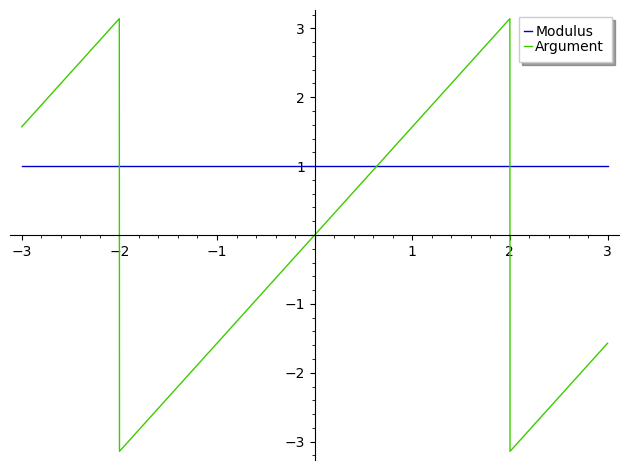
To understand the result, try :
sage: var("a, b")
(a, b)
sage: E0=log(a^b)==log(a^b).log_expand() ; E0
log(a^b) == b*log(a)
sage: E1 =E0.subs([a==I, b==x]) ; E1
log(I^x) == 1/2*I*pi*x
sage: E2 = E1.operator()(*map(exp, E1.operands())) ; E2
I^x == e^(1/2*I*pi*x)
The latter may be easier to grasp in a different form :
sage: E2.rhs().demoivre(force=True)
cos(1/2*pi*x) + I*sin(1/2*pi*x)
Exercise for the (advanced) reader : try and understand :
complex_plot(I^x, (-1, 1), (-1, 1))
 | 2 | No.2 Revision |
As suggested above, a graphical representation gives an easy intuition :
plot([(I^x).abs(), (I^x).maxima_methods().arg()], (x, -3, 3), legend_label=["Modulus", "Argument"])

To understand the result, try :
sage: var("a, b")
(a, b)
sage: E0=log(a^b)==log(a^b).log_expand() ; E0
log(a^b) == b*log(a)
sage: E1 =E0.subs([a==I, b==x]) ; E1
log(I^x) == 1/2*I*pi*x
sage: E2 = E1.operator()(*map(exp, E1.operands())) ; E2
I^x == e^(1/2*I*pi*x)
The latter may be easier to grasp in a different form :
sage: E2.rhs().demoivre(force=True)
cos(1/2*pi*x) + I*sin(1/2*pi*x)
Exercise for the (advanced) reader : try and understand :
complex_plot(I^x, (-1, 1), (-1, 1))
 | 3 | No.3 Revision |
As suggested above, a graphical representation gives an easy intuition :
plot([(I^x).abs(), (I^x).maxima_methods().arg()], (x, -3, 3), legend_label=["Modulus", "Argument"])

To understand the result, try :
sage: var("a, b")
(a, b)
sage: E0=log(a^b)==log(a^b).log_expand() ; E0
log(a^b) == b*log(a)
sage: E1 =E0.subs([a==I, b==x]) ; E1
log(I^x) == 1/2*I*pi*x
sage: E2 = E1.operator()(*map(exp, E1.operands())) ; E2
I^x == e^(1/2*I*pi*x)
The latter may be easier to grasp in a different form :
sage: E2.rhs().demoivre(force=True)
cos(1/2*pi*x) + I*sin(1/2*pi*x)
Exercise for the (advanced) reader : try and understand :
complex_plot(I^x, (-1, 1), (-1, 1))
(-3, 3), (-3, 3))
 | 4 | No.4 Revision |
As suggested above, a graphical representation gives an easy intuition :
plot([(I^x).abs(), (I^x).maxima_methods().arg()], (x, -3, 3), legend_label=["Modulus", "Argument"])

To understand the result, try :
sage: var("a, b")
(a, b)
sage: E0=log(a^b)==log(a^b).log_expand() ; E0
log(a^b) == b*log(a)
sage: E1 =E0.subs([a==I, b==x]) ; E1
log(I^x) == 1/2*I*pi*x
sage: E2 = E1.operator()(*map(exp, E1.operands())) ; E2
I^x == e^(1/2*I*pi*x)
The latter may be easier to grasp in a different form :
sage: E2.rhs().demoivre(force=True)
cos(1/2*pi*x) + I*sin(1/2*pi*x)
Exercise for the (advanced) reader : try and understand :
complex_plot(I^x, (-3, 3), (-3, 3))
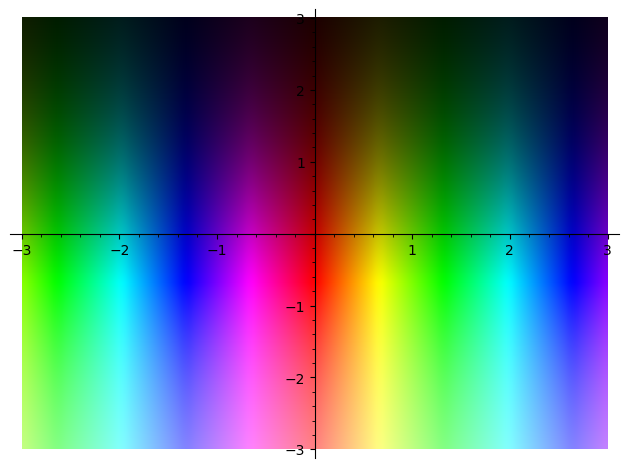
Hint : look up the definitions of exp and trig functions for complexes...
EDIT : The complex_plot is displayed in the editor, but does not appear in the finalized answer. Try it on your machine or Sagecell
HTH,
 | 5 | No.5 Revision |
As suggested above, a graphical representation gives an easy intuition :
plot([(I^x).abs(), (I^x).maxima_methods().arg()], (x, -3, 3), legend_label=["Modulus", "Argument"])

To understand the result, try :
sage: var("a, b")
(a, b)
sage: E0=log(a^b)==log(a^b).log_expand() ; E0
log(a^b) == b*log(a)
sage: E1 =E0.subs([a==I, b==x]) ; E1
log(I^x) == 1/2*I*pi*x
sage: E2 = E1.operator()(*map(exp, E1.operands())) ; E2
I^x == e^(1/2*I*pi*x)
The latter may be easier to grasp in a different form :
sage: E2.rhs().demoivre(force=True)
cos(1/2*pi*x) + I*sin(1/2*pi*x)
Exercise for the (advanced) reader : try and understand :
complex_plot(I^x, (-3, 3), (-3, 3))

Hint : look up the definitions of exp and trig functions for complexes...
EDIT : The complex_plot is displayed in the editor, but does not appear in the finalized answer. Try it on your machine or Sagecell
HTH,
