Tubular surface around curve

edit

Not (yet) a full answer (but see edit below if you are really stuck), but a (high-school level) hint, which, combined with FredericCs big fat one, should give you a solution :

Define the curve as a parametric callable symbolic expression :

t  = SR.var("t")
C(t) = vector([cos(t), sin(t), t/2])

Tangeant :

T(t) = vector(map(lambda u:u.diff(t), C(t)))
# Its norm is time independant...
Tn = T(t).norm().simplify_full()

Normal (= acceleration)

N(t) = vector(map(lambda u:u.function(t).diff(t,2), C(t)))
# Again, time-independent norm :
Nn = N(t).norm().simplify_full()

Binormal :

B(t) = T(t).cross_product(N(t))
# Ditto...
Bn = B(t).norm().simplify_full()

A vector of points where we want to plot Frenet's trihedron

tPts = srange(-pi, 11*pi/10, pi/5)

3D plot of the curve itself :

P1 = parametric_plot3d(C, (-pi, pi), color="black")

Plot the (normed) tangeants :

P2 = sum(map(lambda u:line((C(u),C(u)+T(u)/Tn), color="blue", arrow_head=True),
             tPts))

The normals :

P3 = sum(map(lambda u:line((C(u),C(u)+N(u)/Nn), color="red", arrow_head=True),
             tPts))

The binormals :

P4 = sum(map(lambda u:line((C(u),C(u)+B(u)/Bn), color="green", arrow_head=True),
             tPts))

Now, perusing parametric_plot3d? will show you that this function can plot surfaces having two parameters. This should be more than enough for your goal...

EDIT : Do not read this before doing an honest attempt at finding the solution yourself ; otherwise, you'd lose the benefit of the homework).

This result can be used to get the desired plot. Let's define a description of the normal section of the tube (here a circle of radius r) : the vector (N(t)/Nn, B(t)/Bn) is an orthonormal basis of the plane normal to C(t). Therefore, this description is :

# Radius of a circular-section tube
var("r")
# Parametric desription of the normal section of the tube
Ts(t,theta)=N(t)/Nn*r*cos(theta)+B(t)/Bn*r*sin(theta)

and the description of any point of the tube is :

# A point of the tube
Tu(t,theta)=C(t)+Ts(t, theta)

which can be plotted (along with its center curve) by :

P1 + parametric_plot3d(Tu.subs(r==1/3), (-pi, pi), (0, 2*pi), opacity=0.5)

which should give you something along the lines of :

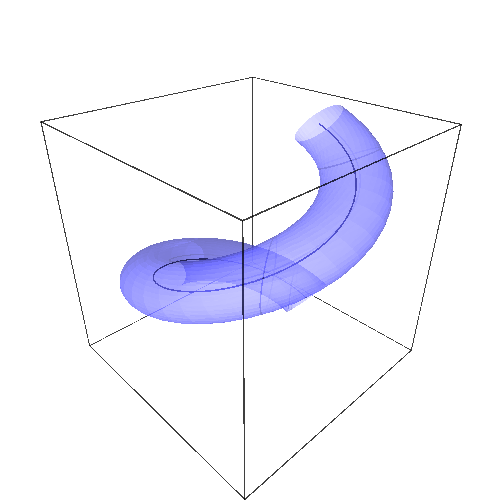
Note that Sage's abilities in differential geometry may give you some radically different solutions. Left as an exercise for the (advanced) reader.

Bonus points : extrapolate to this... ;-)

HTH,