This gets requested from time to time and we should support that!
Not sure the pretty printer can do that, but there are workarounds.
One of them consists in defining "x dot" and "x dot dot" functions,
and to substitute them in the equation.
sage: t, y = SR.var('t, y')
sage: x = function('x')(t)
sage: xdot = function('xdot', latex_name=r'\dot x')
sage: xddot = function('xddot', latex_name=r'\ddot x')
sage: de = y == 2*diff(diff(x, t), t) - 3 * diff(x, t) + 5
sage: dde = de.subs({diff(x, t): xdot(t), diff(diff(x, t), t): xddot(t)})
sage: view(dde)
$$
y = 2 \ddot x\left(t\right) - 3 \dot x\left(t\right) + 5
$$
Even better, when defining a function, you can say what its derivative is.
Using that, start by defining the furthest derivative you'll need
(here xdd for "x dot dot"), then work backwards until you define x.
Then the pretty printer gets things right without the need for subs.
sage: t, y = SR.var('t, y')
sage: xdd = function('xdd', latex_name=r'\ddot x')
sage: xd = function('xd', latex_name=r'\dot x',
....: derivative_func=lambda self, *aa, **ka: xdd(*aa))
sage: x = function('x', derivative_func=lambda self, *aa, **ka: xd(*aa))
sage: de = y == 2*diff(diff(x(t), t), t) - 3 * diff(x(t), t) + 5
sage: view(de)
$$
y = -3 \, \dot x\left(t\right) + 2 \, \ddot x\left(t\right) + 5
$$
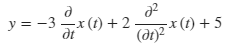
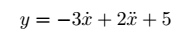

Welcome to Ask Sage! Thank you for your question!
Ideally, add