Plot several functions together
This answers question 1, following @FrédéricC's suggestions.
Summing individual plots:
sage: pcos = plot(cos, (-4, 6), color='steelblue')
sage: psin = plot(sin, (-4, 6), color='purple')
sage: (pcos + psin).show(aspect_ratio=1)
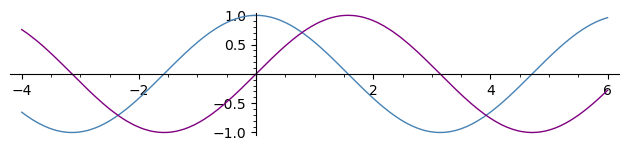
Plotting several functions together (see SageMath documentation on 2D plotting):
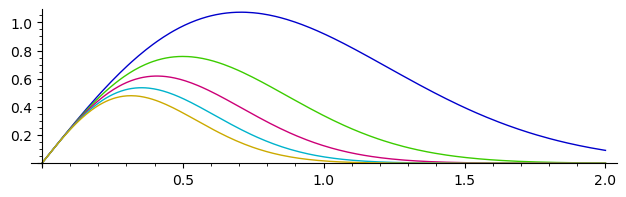
sage: plot([x*exp(-n*x^2)/.4 for n in [1 .. 5]], (0, 2), aspect_ratio=.5)
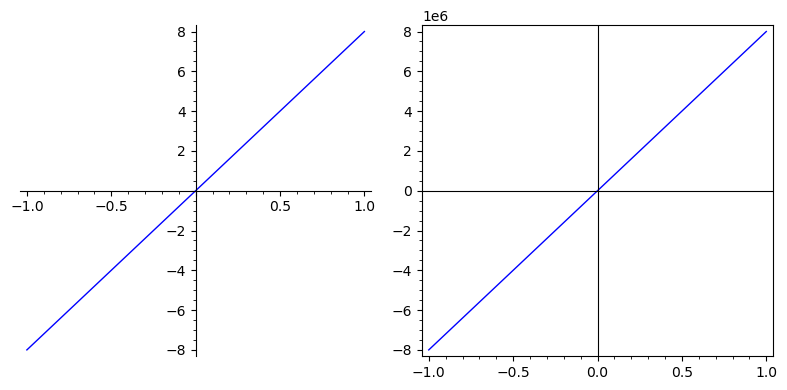
Tick label rendering bug
This answers question 2.
This bug was also reported as
Solving that problem is now tracked at
Until the bug is fixed, a workaround is to plot with a frame,
which will indicate the scaling.
Compare:
sage: p = plot(lambda x: 8e6*x); p
sage: q = plot(lambda x: 8e6*x, frame=True); q
sage: graphics_array([p, q]).show(figsize=(8, 4))
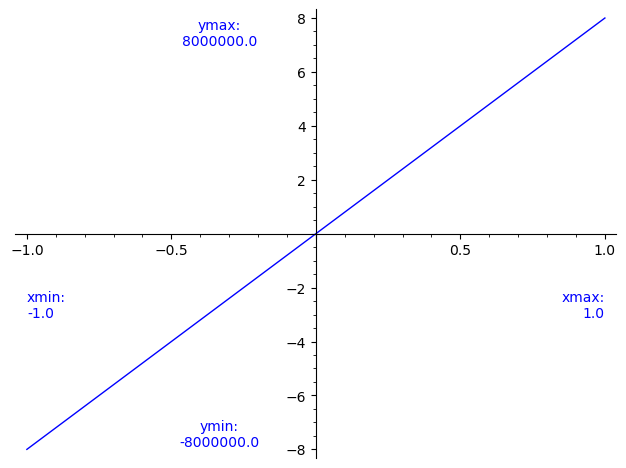
Or you could use the get_minmax_data method to get the
xmin, xmax, ymin, ymax, and somehow add them to the picture as text.
sage: d = p.get_minmax_data()
sage: xa, xb, ya, yb = d['xmin'], d['xmax'], d['ymin'], d['ymax']
sage: xc, yc = mean([xa, xa, xb]), mean([ya, ya, yb])
sage: txa = text(f"xmin:\n{xa}", (xa, yc), horizontal_alignment='left')
sage: txb = text(f"xmax:\n{xb}", (xb, yc), horizontal_alignment='right')
sage: tya = text(f"ymin:\n{ya}", (xc, ya), vertical_alignment='bottom')
sage: tyb = text(f"ymax:\n{yb}", (xc, yb), vertical_alignment='top')
sage: pt = p + sum([txa, txb, tya, tyb])
sage: pt
Launched png viewer for Graphics object consisting of 5 graphics primitives
Rounding errors in floating-point calculations
This answers question 3.
Problematic plot
The exponential function on [0, 1], rescaled to [-1, 1].
sage: h(x) = exp(x/2 + 1/2)
Its Chebyshev approximation of order 11:
sage: f(x) = 1.648721270700127734695199 + 0.8243606353500639704213267*x + 0.2060901588375456897278408*x^2 + 0.03434835980625555348009372*x^3 + 0.004293544975435477755738488*x^4 + 0.0004293544975550920330337524*x^5 + 3.577954294118110098524956e-05*x^6 + 2.555681612268918733452545e-06*x^7 + 1.597272498430465439987321e-07*x^8 + 8.873762489265668731711247e-09*x^9 + 4.462222789173961848447732e-10*x^10 + 2.027323563290198480646098e-11*x^11
The quality-of-approximation function: their difference:
sage: g(x) = f(x) - h(x)
The problematic plot:
sage: pg = plot(g, color='steelblue')
sage: pg.show(frame=True, figsize=(7, 2))
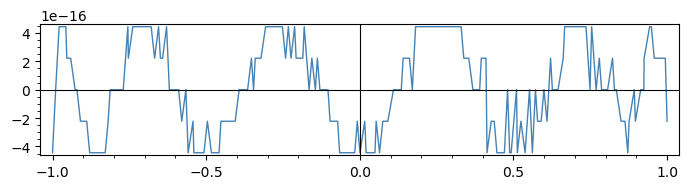
Plotting uses floating-point computations!
The plot in the question seems to be taking only 7 y-values.
This plot's goal is to visualise a quality of approximation
by plotting the difference f(x) - h(x) of two almost-equal
functions (f is an approximation of h of high quality).
Of course, this means the function g = f - h takes extremely
small values. The way they are computed becomes important!
Knowing how the plot command works helps understand
what is going on: it samples 200 floating-point values in the
plotting interval and computes the value of the function at
these points. These are floating-point computations, with
53 bits of precision, which is roughly 15 or 16 decimal digits.
Here, both f and h have values that are roughly on the
order of one, and their difference is on the order of 1e-16.
(Furthermore f itself is a polynomial, so each f(x) is
a linear combination of twelve powers of x.)
In the end each g(x) is the sum of terms of various sizes,
summed in a certain order, resulting in a value very close
to the precision of some of the numbers being summed.
It becomes hard to put much trust our output.
Arb to the rescue
A general suggestion for dealing with precision issues is
to use Arb for arbitrary precision calculations.
In Sage, Arb can be used via RealBallField and ComplexBallField.
The Sage documentation and Ask Sage have a few examples.
For the purpose of this question, we can use evaluation of polynomials
with integer or rational coefficients on real or complex balls.
This is a recent feature of Arb, even more recently available in Sage
(thanks to the work at Sage Trac ticket 30652)
In fact it is only part of Sage since version 9.3.beta0.
Here is one way to use that.
Define the coefficients of the Chebyshev polynomial approximation.
sage: cc = (1.648721270700127734695199,
....: 0.8243606353500639704213267,
....: 0.2060901588375456897278408,
....: 0.03434835980625555348009372,
....: 0.004293544975435477755738488,
....: 0.0004293544975550920330337524,
....: 3.577954294118110098524956e-05,
....: 2.555681612268918733452545e-06,
....: 1.597272498430465439987321e-07,
....: 8.873762489265668731711247e-09,
....: 4.462222789173961848447732e-10,
....: 2.027323563290198480646098e-11)
Turn them into rationals:
sage: ccc = [QQ(c.as_integer_ratio()) for c in cc]
Define the polynomial ring over QQ with variable x:
sage: P = QQ['x']
Define the Chebyshev approximation as a polynomial over QQ:
sage: ff = P(ccc)
Define the quality-of-approximation function:
sage: def gg(x):
....: return ff(x) - exp(x/2 + 1/2)
Define a real ball field with sufficient precision (here we take 1000 bits).
sage: R = RealBallField(1000)
Define an alternative version of the quality-of-approximation function
using real balls:
sage: def ggg(x):
....: return gg(R(x))
Plot:
sage: pggg = plot(ggg, color='purple)
sage: pggg.show(frame=True, figsize=(7, 2))
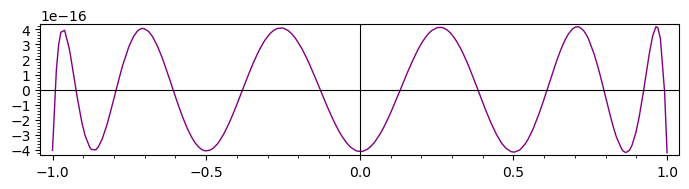
Compare to the original plot:
sage: p = plot(f(x) - exp(x/2 + 1/2), x, frame=True, figsize=(7, 2))
sage: q = plot(gg, color='steelblue', frame=True, figsize=(7, 2))
sage: (p + q).show(figsize=(7, 2))
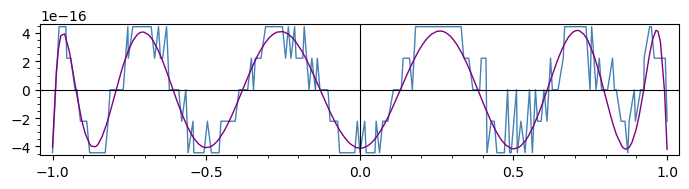
This comparison shows that despite its jaggedness,
the low-resolution plot was still giving an indication
of the variations of the difference between the
approximating and the approximated functions.








For 1, use P+Q where P and Q are two plots. Or use a sequence of functions as argument of plot.
Question 2 was also reported as
Solving that problem is now tracked at
For question 3, a concrete example would make it easier to explore the question.
To give a general suggestion, computing in arbitrary precision with Arb, via
RealBallFieldorComplexBallField, might be a way to alleviate such problems.3.Example: plot(p(x)-exp(x),x) where p(x) = Chebyshev approximation of exp(x) for degree>10
Please provide complete code, including defining
p(x), for anyone to copy-paste.This saves effort and time when exploring the question.
Ideally, edit your question to add the code.