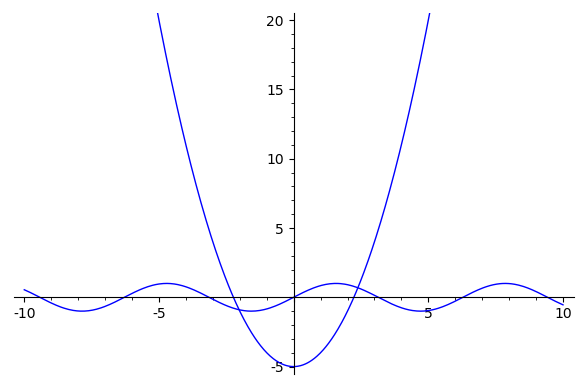
plot of sine, parabola intersection works but solve makes no sense
When I plot a sine and parabola I get two obvious intersections
plot(x^2-5,-10,10,ymax=20) + plot(sin(x),-10,10)
But when I solve to get the two numeric x values, the answer makes no sense.
solve(x^2-5==sin(x),x)
[x == -sqrt(sin(x) + 5), x == sqrt(sin(x) + 5)]