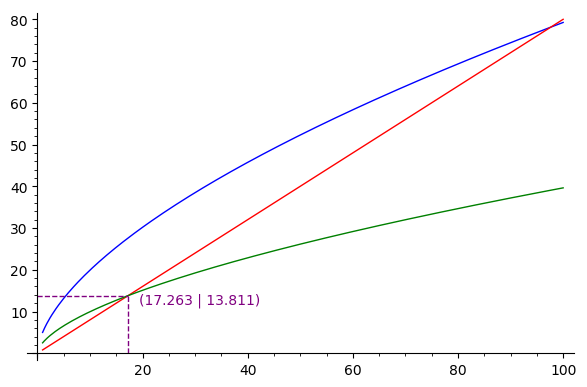
Running the Solow Model in Sage and Plotting it.

edit

A modest proposal (with a few suggestions) :

k, alpha, A, delta, s, c=var('k, alpha, A, delta, s, c')
#Initial Values
# k=10 # It's a variable !
s=0.5
A=5
alpha=0.6
delta=0.8
# Equations of Interest : define FUNCTIONS (much cleaner, lighter, independent of the variable name)
f(k)=A*k^alpha    
k1(k)=f(k)-(1-delta)*k
invest(k)=s*f(k)
dk(k)=delta*k
# Visualizing the Solow Model ; lighter notations allowed by functions
prod=plot(f,(1,100),color='blue')
lom=plot(dk,(1,100),color='red')
savings=plot(invest,(1,100),color='green')
#  Curves intersection.
# Symbolic way :
Sol=(dk(k)==invest(k)).log().log_expand().solve(k) # Avoid the trivial nonsensical solution
print("invest(k)==delta*k for {}".format(Sol))
# SolN=Sol[0].rhs().n()
# Alternate way to solve numerically
SolN=SR(find_root(invest(x)-dk(x),1,100)) # Conversion to SR to allow use og .n()...
Sav=invest(k=SolN)
print("Intersection at ",(SolN,Sav))
prod+lom+savings+line([(SolN,0),(SolN,Sav),(0,Sav)], linestyle="dashed")+\
text(" k={}, invest={}".format(SolN.n(digits=3), Sav.n(digits=3)),(SolN,Sav),\
     horizontal_alignment="left", vertical_alignment="top", color="black")

HTH,