How to make a permutation of a card problem and compute its order?
Risto arranged card deck cards first by suits and when by numerical values. After that he started to deal cards to piles such that every pile contained equal number of cards. As he had no cards, he collected the piles and started to deal the deck in the similar process. It took time but Risto continued doealing. Suddenly the cards were on their original order.
Task
Program knows the number of cards, number of piles, and the number of cards to be put on every pile. The task is to compute how many times Risto must collect the cards such that the cards are on their original order.
Cards have been dealt one at time and the cards have been put one the piles on the same order. As one has dealt every card, piles are gathered together such that the first pile goes to the most bottom in the pile. After that the cards in the new order will be piled and combined ia a similar way. Finally the order of cards will be as in the start.
In the next picture one can see a process if there are four cards and two piles. In the first pine one always adds two cards and on the second pile one adds one card. In this case a pile contains three cards and on the second deal there remains only one card that goes to the first pile.
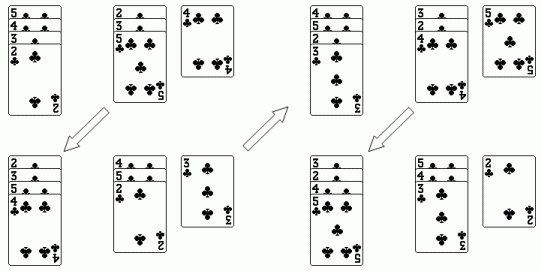
After four arrangements the order of the cards is as in the beginning. This means it takes four rounds to get cards to their original order.
How can I solve the problem by computer if the data of cards are as in https://www.ohjelmointiputka.net/tied... ? The first number is the number of cards, then the number of piles and the next the number of cards one adds to every pile.
The format of the answer
Every line contains - number of cards - number of rounds to get cards into the original order.
For example, the answer to the example is 4 4
I think one could make some kind of permutation and compute its order. But how can I implement it?
