how do i plot a parabola in the x=2 plane?
I apologize, for I am very new to sage. Here is what I input; the error was that y was not defined.
f(x)=x^2
P=implicit_plot3d(lambda x,y,z:x-2,(-2,2),(-2,2),(-2,8))
plot(f)+plot3d(P)
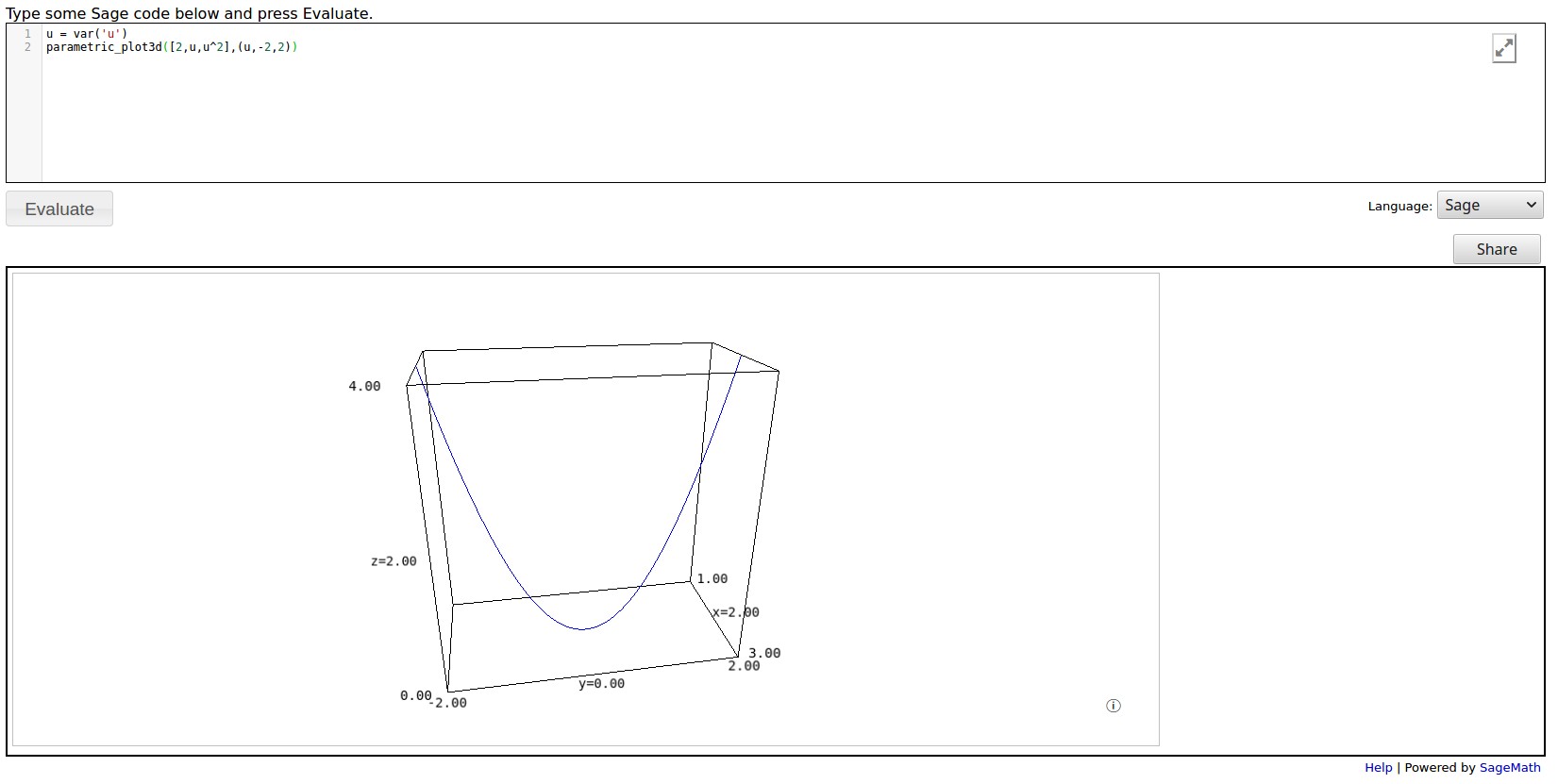

You can use
var('y')to defineyas a variable, and similarly forz.