How to draw a graph whose vertices are elements of permutation group
How to write the following program in SageMath:
Consider the Permutation Group $S_3$.
The elements of $S_3$ are $e,(12),(13),(23),(123),(132)$.
I want to draw a graph $G$ whose members are the elements of $S_3$ and two vertices $x,y$ are adjacent if and only if $xy\neq yx$.
I am stuck in doing the following things:
- How to call the elements of $S_3$ through a loop?
- How to draw the graph $G$ ?
I can check whether they commute or not but I am stuck in the two things. Is there any way to write the code in SageMath?
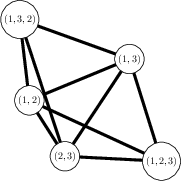
As an example if I input $S_3$ I want to get the following graph
$G=Graph({1:[2,3,4,5],2:[1,3,4,5],3:[1,2,4,5],4:[1,2,3],5:[1,2,3]})$
Any help will be highly appreciated.