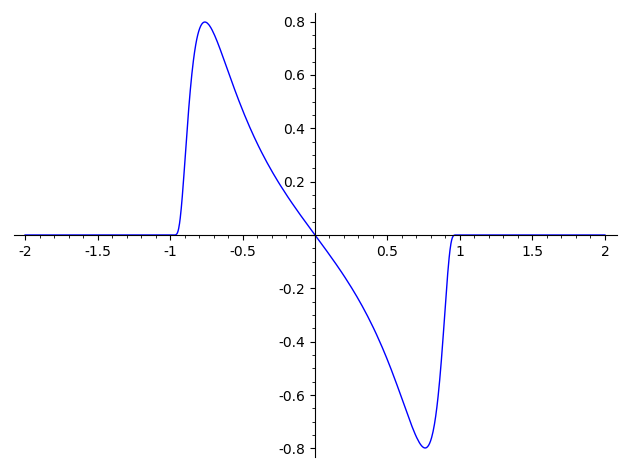
Plotting derivative of bump function
I wish to plot the derivative of the piecewise function equal to exp((1−x2)−1) on (-1, 1) and 0 everywhere else (just as an example). I attempted this by defining to define in sage
f(x) = piecewise([(-oo, -1), 0], [(-1, 1), exp(-1/(1 - x^2)), [(1, oo), 0]]
and then let g = diff(f(x), x)). When i try to evaluate g at various values (for example 0.3), I get 0.333237077156224*(0, 0, 0) + 0.333237077156224, and the number that appears is not only incorrect (in that it is not the derivative it ought to equal), but the expression that appears can't be turned into a single number. My ultimate objective is to obtain plots of various linear combinations of such expressions, so what would be the best way to go about doing this? In addition, what exactly is going on here?