Numerical integration and plot failing
I have a function which can be efficiently calculated on some interval on the real line and if I feed Sage with concrete arguments, Sage gives concrete numerical values. Nevertheless, if I try to integrate it numerically (or plot it), something goes terribly wrong and Sage is not able to calculate the values.
In my case I get the error message
negative number cannot be raised to a fractional power
The function itself is a solution to the cubic equation so it involves square root and a cubic root.
is it some bug in sage and if there is some workaround?
MINIMAL NON_WORKING EXAMPLE
y = var('y')
z = var('z');
cauchy = y.substitute(solve(z*y^3 +y^2 - 2*z*y+2, y)[0])
def F(u):
return arg(cauchy).substitute(z=u).n()
numerical_integral(F, 1, 2)

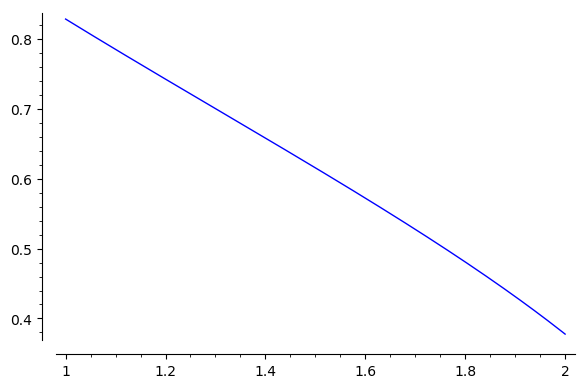

Indeed :
Therefore, this function can be evaluated. But :
... not in
plot. Trying to plot symbolically yelds :A bug, IMHO