Plot points in loglog

asked 2019-05-10 12:32:54 +0100

LeChuck42
13 ●2

updated 2019-05-10 19:31:22 +0100

Iguananaut
1708 ●8 ●33 ●55

Hi I'm trying to plot a function with loglog scaling. However the result seems to have very few plot points. I'm using Sage 8.7 on Windows.

image description

Is this a bug or am I doing something wrong?

Cheers!

edit retag flag offensive close merge delete

Comments

I don't know an immediate answer off the top of my head, but it looks like it has to do with how the plotted points are being sampled. For whatever reason it's not finding your inflection point and adding extra points around it to make it look smoother; instead you just get this sharp inflection. BTW, it would help if you posted the text of your code in the question so it can easily be copy/pasted.

Iguananaut ( 2019-05-10 19:08:11 +0100 )edit

add a comment

2 Answers

Sort by » oldest newest most voted

answered 2019-05-11 22:32:52 +0100

slelievre
17704 ●22 ●160 ●350 http://carva.org/samue...

updated 2019-05-12 13:07:54 +0100

It would seem plots in log scale use a sampling done in the non-log scale...

Since plots only 200 plot points by default, the sampling in non-log scale means that for a log-scale plot, most plot points are near the end, and they are very scarce in the first 3/4 of the plot.

A workaround, as suggested in @Iguananaut's answer, is to use more plot points.

Using 800 plot points already gives a much smoother curve here:

sage: tau = RDF.pi()*2
sage: out2 = lambda r, c: lambda f: ~(1 + (tau*f*r*c)^2)
sage: plot(out2(15, 2.7e-9), (10, 500e6), scale='loglog', plot_points=800)
Launched png viewer for Graphics object consisting of 1 graphics primitive

There was a problem I thought looked similar: the x-range and y-range for a plot are chosen slightly wider than the actual range of x-values and y-values that occur in the plot, and sometimes in log scale it looks like this "slightly wider" is chosen in non-log scale, giving a wrong aspect. See

Ask Sage question 26637: Plot boxes have jumpy xy ranges in log scale

edit flag offensive delete link

Comments

Yes, I tried displaying the plot points with plot(out(15, 2.7e-9)^2, (10, 500e6), scale='loglog', markers="+") and there are lots of points in the section > 10^7 suggesting the selection of points is done in non-log scale. I think this is really confusing and probably should be fixed in a future release. Marked as answer, because of this. But thanks to @Iguananaut for the workaround!

LeChuck42 ( 2019-05-13 10:56:21 +0100 )edit

"It would seem plots in log scale use a sampling done in the non-log scale..." I wondered if that might be the case myself. If so, should we open a ticket for this? Seems buggy to me.

Iguananaut ( 2019-05-13 17:35:02 +0100 )edit

This should definitely be fixed. Maybe as part of

Sage Trac ticket 15320: plot_semilogx(1/log(x),10,10^15) should look like plot(1/x,1,15)

slelievre ( 2019-05-14 23:12:49 +0100 )edit

add a comment

answered 2019-05-10 19:23:11 +0100

Iguananaut
1708 ●8 ●33 ●55

I was able to obtain a reasonably nice plot with:

plot(out(15, 2.7e-9), (10, 500e6), scale='semilogx', plot_points=2000)

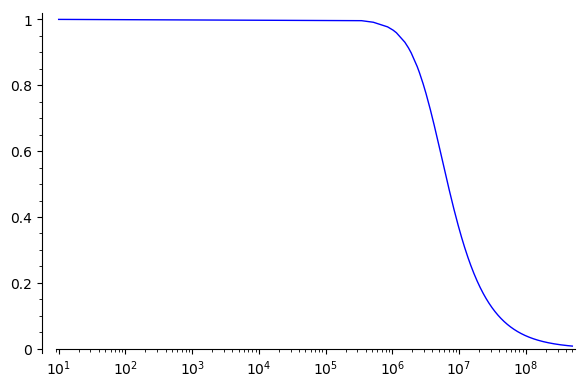
image description

Another way you could do it is break it up into multiple plots, with one plot adding more points just around the inflection point, like:

f_0 = out(15, 2.7e-9)
P = plot(f_0, (10, 3e5), scale='semilogx') # Just eyeballing it
P += plot(f_0, (3e5, 3e6), scale='semilogx')
P += plot(f_0, (3e6, 5e8))
P

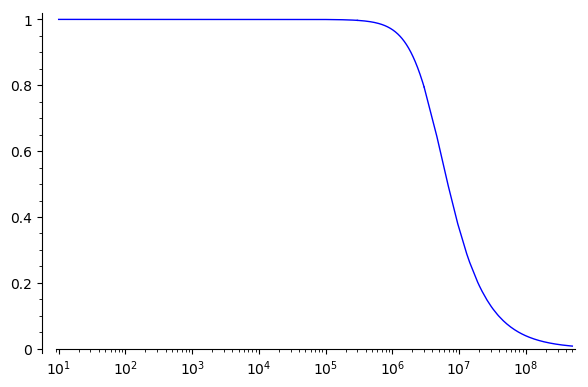
image description

which looks a tiny bit smoother.

Regardless, it could be nice if the automatic interpolation were better in this case. It's possible some other parameters could be adjusted to improve it but I'm not sure.

edit flag offensive delete link

Comments

I'll also add that since most of that initial level part is not very interesting you might also consider just cropping the plot by having the x-axis start around 10e4, 10e5 or so...

Iguananaut ( 2019-05-10 19:24:26 +0100 )edit

add a comment

Your Answer

Please start posting anonymously - your entry will be published after you log in or create a new account.

Add Answer

Plot points in loglog

Comments

2 Answers

Comments

Comments

Your Answer

Question Tools

Stats

Plot points in loglog edit

Comments

2 Answers

Comments

Comments

Your Answer

Question Tools

Stats

Plot points in loglog